[All in One(2조)] 프로젝트로 배우는 데이터사이언스

Study/CODE 2기 [프로젝트로 배우는 데이터사이언스]

[All in One(2조)] 프로젝트로 배우는 데이터사이언스_2주차

23_오현정 2024. 3. 18. 17:08

2. 1. 1 당뇨병 데이터셋 미리보기

0. 데이터 구성

- Pregnancies : 임신 횟수

- Glucose : 2시간 동안의 경구 포도당 내성 검사에서 혈장 포도당 농도

- BloodPressure : 이완기 혈압 (mm Hg)

- SkinThickness : 삼두근 피부 주름 두께 (mm), 체지방을 추정하는 데 사용되는 값

- Insulin : 2시간 혈청 인슐린 (mu U / ml)

- BMI : 체질량 지수 (체중 kg / 키(m)^2)

- DiabetesPedigreeFunction : 당뇨병 혈통 기능

- Age : 나이

- Outcome : 768개 중에 268개의 결과 클래스 변수(0 또는 1)는 1이고 나머지는 0이다.

1. 라이브러리 로드하기

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

%matplotlib inline

데이터 분석을 위한 pandas, 수치 계산을 위한 numpy, 시각화를 위한 seaborn과 matplotlib.pyplot을 로드한다.

2. 데이터 로드하기

df = pd.read_csv("/content/drive/MyDrive/diabetes.csv")
df.shape

(768, 9)

read_csv를 이용해 csv 파일을 불러온다. 나는 MyDrive 폴더에 diabetes.csv 파일을 저장해놓았기 때문에 "/content/drive/MyDrive/diabetes.csv" 경로를 통해서 파일을 불러온다.

df.head()

먼저, head()를 이용해 위에서 5개의 데이터만 미리 확인해 살펴본다.

df.info()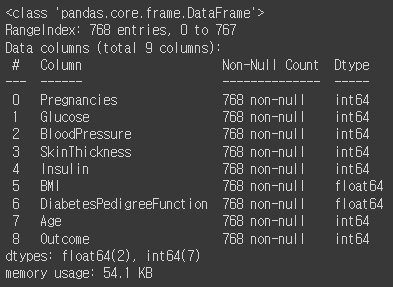

info()를 이용해 데이터 타입, 결측치, 메모리 사용량 등의 정보를 확인한다. BMI와 DiabetesPedigreeFunction은 float의 데이터 타입을 가지며, 이 둘을 제외한 나머지 데이터들은 int의 데이터 타입을 가진다.

df_null = df.isnull()
df_null.head()

df.isnull()을 이용해 데이터프레임의 각 값에 null(결측치)이 존재하는지 확인한다. null이 존재하면 True, null이 존재하지 않으면 False로 나타낸다.

df_null.sum()

df_null.sum()을 이용해 각 데이터 별 null의 개수를 확인해 본 결과, null은 존재하지 않는 것을 확인할 수 있었다.

df.describe()

df.describe()를 이용해 수치 데이터에 대한 요약을 확인한다.

- count(개수) : 데이터프레임에서 비어 있지 않은 값의 개수

- mean(평균) : 데이터의 평균값

- std(표준 편차) : 데이터의 표준 편차

- min(최솟값) : 데이터의 최솟값

- 25%(25번째 백분위수) : 데이터의 25번째 백분위수

- 50%(중앙값) : 데이터의 중앙값으로, 데이터를 크기 순으로 정렬했을 때 가운데 위치한 값

- 75%(75번째 백분위수) : 데이터의 75번째 백분위수

- max(최댓값) : 데이터의 최댓값

feature_columns = df.columns[:-1].tolist()
feature_columns

가장 마지막에 있는 Outcome은 label 값이기 때문에 제외하고 학습과 예측에 사용할 컬럼을 만들어 준다.

2. 1. 2. 결측치 보기

1. 결측치 시각화

(1) 결측치 데이터프레임 만들기

값을 요약했을 때 최솟값이 0이 나오는 데이터 들이 있는데, 인슐리이나 혈압 등의 값은 0이 나올 수가 없기 때문에 이러한 값들은 결측치라고 볼 수 있다. 따라서, 0인 값을 결측치로 처리하고 시각화 해 볼 것이다.

cols = feature_columns[1:]
cols

Pregnancies를 제외한 모든 데이터들은 0값이 결측치라고 볼 수 있기 때문에 feature_columns 중에서 첫번째 열을 빼고, 나머지 수치들을 cols 변수로 지정해 준다.

df_null = df[cols].replace(0, np.nan)
df_null = df_null.isnull()
df_null.sum()

0값을 결측치라 가정하고 결측치 여부를 나타내는 데이터프레임을 만든다.

df_null.mean() * 100

df_null.mean()에 100을 곱해줘서 각 수치별 결측치의 비율을 구해준다.

(2) 결측치 막대 그래프로 시각화

df_null.sum().plot.barh()

df_null.sum()을 이용해 구한 결측치의 개수를 plot.barh()를 이용해 막대 그래프로 시각화 한다.

(3) 결측치 히트맵으로 시각화

plt.figure(figsize=(15, 4))
sns.heatmap(df_null, cmap="Greys_r")

결측치를 heatmap으로 시각화 한다. True 값은 1, False 값은 0이다. plt.figure()를 이용해 시각화 그래프의 사이즈를 조절할 수 있고, cmap 옵션을 지정해 색상을 grayscale로 변경할 수 있다.

2.1.4 두 개의 변수를 정답값에 따라 시각화 해보기

파이썬에서 활용할 수 있는 다양한 데이터 시각화 플롯 가운데 다음에서 2차원 복합데이터에 활용하는 플롯들을 직접 실행해보자. 만약 데이터가 2차원이고 실수 값, 카테고리 값이 섞여 있다면 기존의 플롯 이외에도 다음과 같은 분포 플롯들을 이용할 수 있다.

그래프 유형설명

그래프 유형	설명
Barplot	범주형 변수에 대한 평균 또는 합을 막대 형태로 나타내는 그래프이다. 각 막대는 변수의 값에 따라 높이를 나타낸다.
Boxplot	데이터의 분포와 이상치를 시각적으로 보여주는 그래프이다. 데이터의 최솟값, 제 1사분위수, 중앙값, 제 3사분위수, 최댓값을 표시한다.
Pointplot	각 변수의 평균 또는 중앙값을 점으로 나타내는 그래프이다. 점 사이의 선은 추정된 변화의 크기를 나타낸다.
Violinplot	데이터 분포를 바이올린 형태의 곡선으로 나타내는 그래프이다. 박스 플롯과 커널 밀도 추정 그래프를 결합하여 데이터의 분포와 이상치를 시각적으로 보여준다.
Stripplot	각 변수의 값에 따라 점을 놓는 그래프이다. 범주형 변수에 따라 점이 겹치지 않도록 조절하여 개별 데이터 포인트를 시각적으로 나타낸다.
Swarmplot	Stripplot과 유사하지만, 데이터 포인트가 겹치지 않도록 약간의 랜덤화를 적용하여 여러 개의 범주형 변수에 대한 개별 데이터 포인트를 나타낸다.

다음에서 두 개의 변수를 정답값(Outcome)에 따라 여러가지 플롯으로 시각화 해보자.

2.1.3 훈련과 예측에 사용할 정답값을 시각화로 보기

df["Outcome"].value_counts()

df["Outcome"] -> 모든 행의 Outcome의 값을 나타낸다. ".value_counts()"을 뒤에 붙여 데이터프레임의 outcome의 갯수를 세서 보여준다. 여기서 0은 발병하지 않는, No의 값이고, 1은 발병하는 케이스로 Yes의 의미를 나타낸다.

df["Outcome"].value_counts(normalize=True)

value_counts의 괄호 안에 normalize=True를 적게 되면 비율을 알 수 있다. normalize는 정규화라는 뜻으로 여기서는 0과 1이 이루는 비율을 확인할 수 있다.

outcome 속 0의 비율이 약 65%, 1의 비율이 약 35%이다.

데이터를 비율로 나타내면서 데이터 타입이 실수형인 float으로 바뀐 것을 확인할 수 있다.

df.groupby(["Pregnancies"])["Outcome"].mean()

groupby 함수는 판다스 내부 함수로 별도의 데이터를 처리하기 위해 사용하는 함수이다. 여기서는 임신 횟수와 당뇨병 발병 여부의 관계를 보기 위해 지정했다. ".mean()"을 덧붙여 임신 횟수 별 발병 확률을 나타낸다.

df_po = df.groupby(["Pregnancies"])["Outcome"].agg(["mean", "count"]).reset_index()
df_po

임신횟수가 12~13을 넘어가자 확률 데이터가 약간 미심쩍다. 케이스의 수를 알아보기 위해서 .agg(["mean", "count"])를 추가하여 이전의 임신 횟수별 평균 발병률과 더불어 그 발병률의 케이스 수를 나타내준다.

df_po.plot()

plot함수를 통해 그룹바이 함수로 그룹화한 임신횟수 별 발병 횟수와 평균값에 대한 비율을 그래프로 시각화해보자.

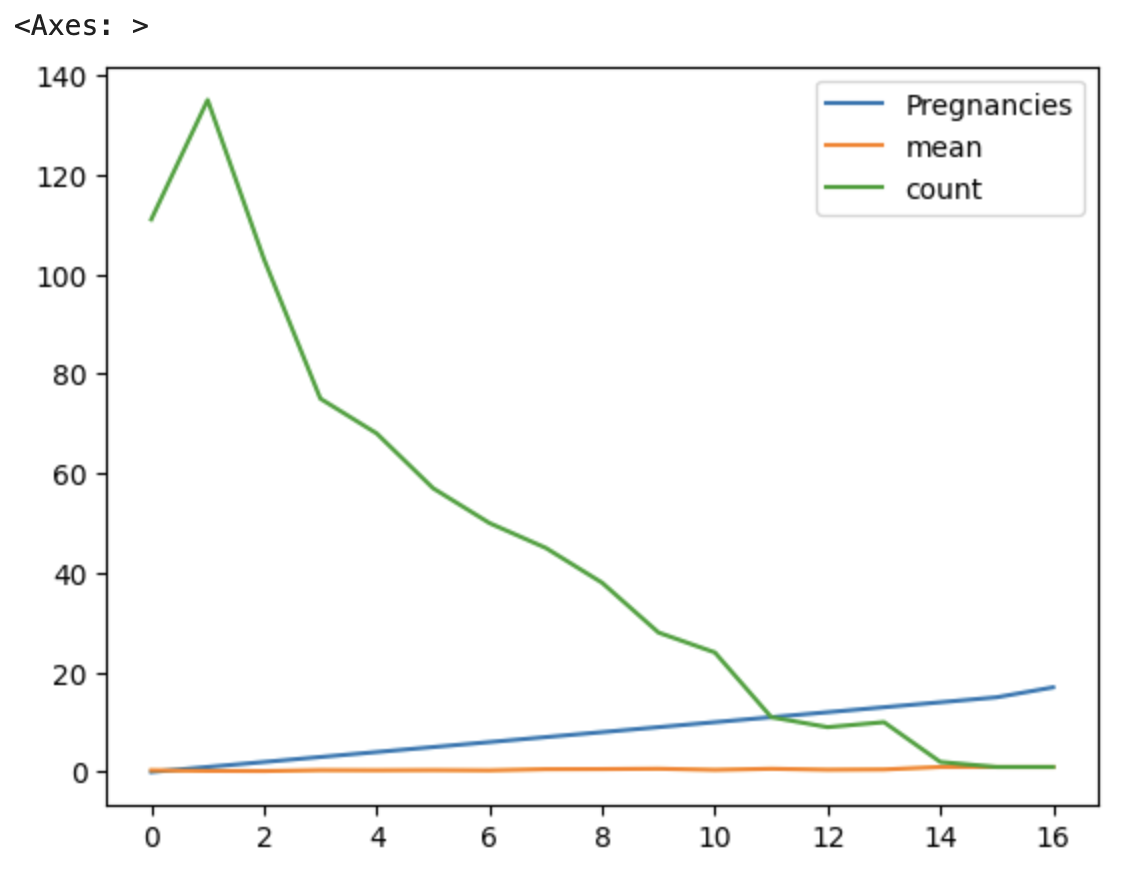
그래프를 보면 초록색 발병 횟수 값이 낮아지는 것을 확인할 수 있다. 그래서 강의에서는 수치가 다 다르므로 의미있는 결과 도출이 어렵다고 생각하여 임신횟수에 대한 발병률 그래프를 그리기로 한다. 그렇게 하기 위해서는 기존 df_po.plot에서 mean의 값만 보면 된다.

df_po["mean"].plot()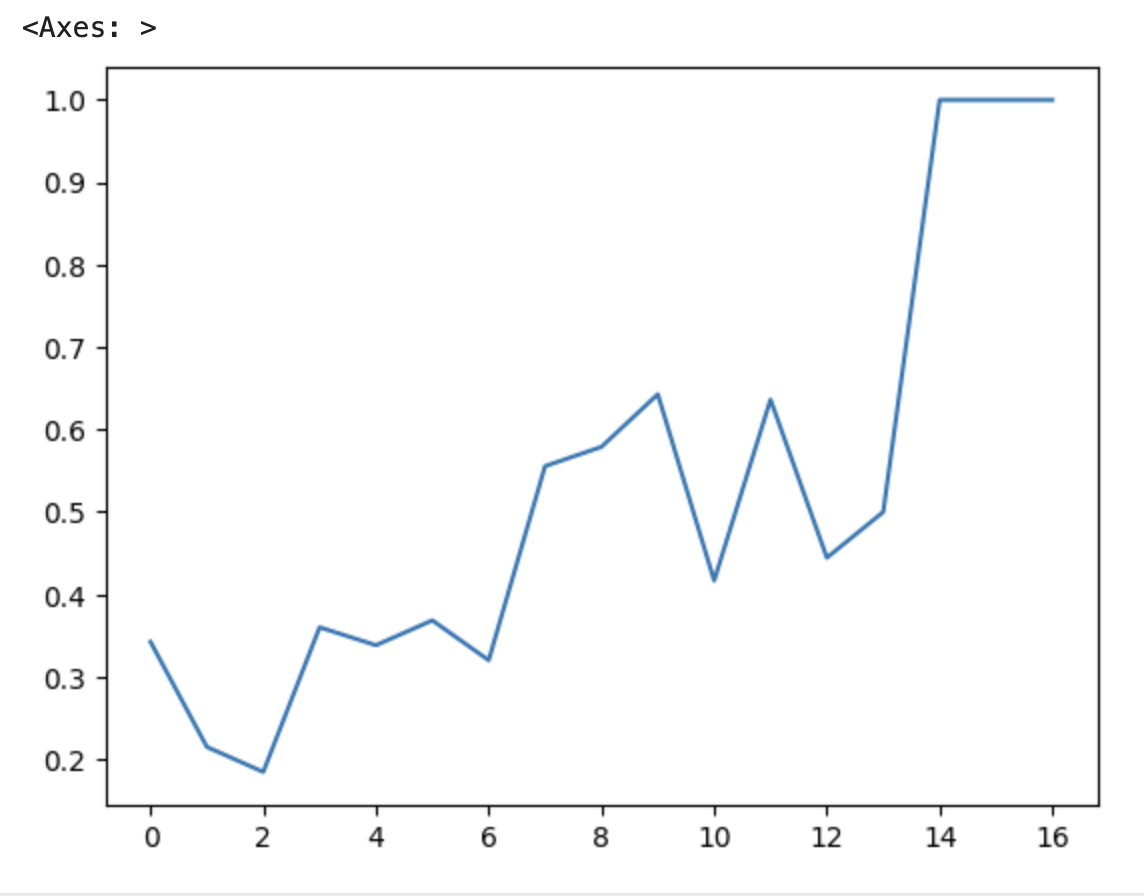

가장 기본 형태인 꺾은선 그래프가 나온다. 그러나 임신 횟수는 연속적인 숫자가 아닌 정수형 자료이므로 막대 그래프로 보는 것이 더 편하다고 할 수 있다. 그러면 막대 그래프 형식으로 그래프를 출력해보자.

df_po["mean"].plot.bar(rot=0)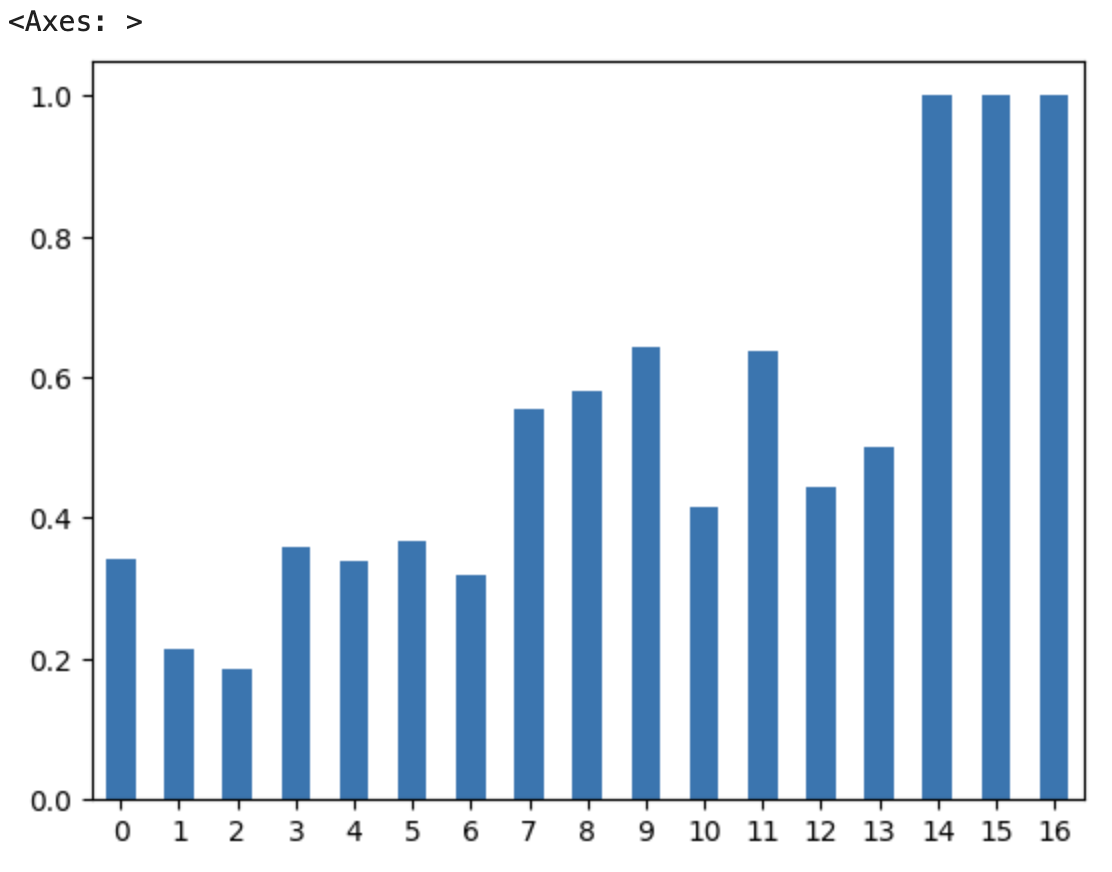

막대 그래프를 그리기 위해 위에 있던 기존 코드에 ".bar()"를 추가한다. 그러면 이런 막대 그래프가 생겨난다.

1) barplot

먼저 batplot이다. barplot 은 카테고리 값에 따른 실수 값의 평균과 편차를 표시하는 기본적인 바 차트를 생성한다. 평균은 막대의 높이로, 편차는 에러바(error bar)로 표시한다.

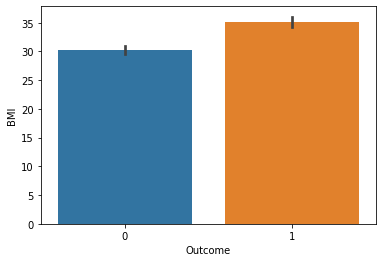
① 당뇨병 발병에 따른 BMI 수치 비교

sns.barplot(data=df, x="Outcome", y="BMI")

※ 검은색 막대는 데이터의 95% 신뢰 구간(ci=95)

② 당뇨병 발병에 따른 포도당(Glucose)수치를 비교

sns.barplot(data=df, x="Outcome", y="Glucose")

③ Insulin 수치가 0 이상인 관측치에 대해서 당뇨병 발병을 비교

sns.barplot(data=df, x="Outcome", y="Insulin")

95%의 신뢰구간을 나타내는 검은색 막대의 길이가 확연히 다른 걸로 보아 신뢰구간의 차이가 큰 것을 알 수 있다. 신뢰 구간의 크기가 클수록 통계적 불확실성이 더 크다는 것을 의미한다. 따라서 해당 추정치의 신뢰성이 낮아지므로 데이터를 더 신중하게 해석해야 하고 추가적인 정보나 데이터가 필요하다.

④ 임신횟수에 따른 당뇨병 발병 비율 비교

sns.barplot(data=df, x="Pregnancies", y="Outcome")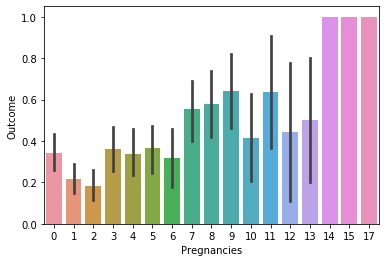

⑤ 임신횟수(Pregnancies)에 따른 포도당(Glucose)수치를 당뇨병 발병여부(Outcome)에 따라 시각화

위에서 임신횟수와 당뇨병 발병을 비교했다면 이번에는 포도당 수치까지 3가지 정보를 한 그래프로 나타내보자.

이때 barplot의 파라미터 중 'hue'를 사용하면 된다. 이 파라미터는 데이터를 추가적으로 그룹화하여 시각화할 때 는 것으로 주로 범주형 변수를 지정하며, 각 범주별로 서로 다른 색상으로 구분하여 데이터를 시각화할 수 있다. 밑에 생성된 그래프를 보면 임신횟수와 포토당 수치 그래프가 발병 유무에 따라 색이 다르게 2개의 그래프로 표현될 것 볼 수 있다.

sns.barplot(data=df, x="Pregnancies", y="Glucose", hue="Outcome")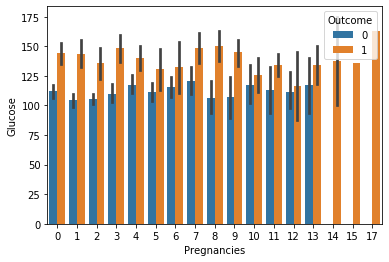

⑥ 임신횟수(Pregnancies)에 따른 체질량지수(BMI)를 당뇨병 발병여부(Outcome)에 따라 시각화

sns.barplot(data=df, x="Pregnancies", y="BMI", hue="Outcome")

⑦ 임신횟수(Pregnancie)에 따른 인슐린 수치(Insulin)를 당뇨병 발병여부(Outcome)에 따라 시각화

# 인슐린 수치에는 결측치가 많기 때문에 0보다 큰 값에 대해서만 그림

sns.barplot(data=df[df["Insulin"] > 0],
            x ="Pregnancies", y="Insulin", hue ="Outcome")

※ barplot()과 bar()의 차이점

1. bar()는 Matplotlib 라이브러리에서 제공하는 함수이고 barplot()은 Seaborn 라이브러리에서 제공하는 함수이다.

2. bar()는 사용자가 데이터와 스타일을 모두 정의해야 하는 반면, barplot()은 데이터 프레임을 직접 전달하고 필요한 경우 Seaborn이 데이터를 요약하고 그래프를 그리는 데 필요한 모든 작업을 수행한다.

3. bar()는 기본적인 시각화만 가능하며 통계적 추정치 계산을 지원하지 않는 반면, barplot()은 기본저그올 각 범주에 대한 통계량과 신뢰구간을 계산하여 표시할 수 있다. 따라서 데이터를 시각적으로 요약하고 범주간의 비교에 용이하다,

2) boxplot

위의 임신횟수 & 인슐린 수치 & 당뇨병 발병 여부 그래프를 이번에는 boxplot을 활용해 시각화해보자. boxplot은 데이터 분포의 대략적인 모양, 중앙값과 사분위수 등을 한눈에 파악할 수 있어 데이터의 대략적인 분포를 비교하거나 이상치를 확인할 때 많이 사용한다. 총 상자,수염,이상치,중앙값 네 가지 요소로 구성되어 있고 자세한 설명은 다음을 참고하자.

상자 (Box): 상자의 하단면은 제 1 사분위수(Q1)를 나타내고, 상단면은 제 3 사분위수(Q3)를 나타낸다. 상자의 높이는 데이터의 사분위수 범위(IQR, Interquartile Range)를 나타낸다.
수염 (Whiskers): 상자 위와 아래에 있는 선분으로, 대부분의 데이터 포인트가 있는 범위를 나타낸다. 일반적으로 상자 밖의 데이터 포인트 중에서 1.5*IQR 이상 떨어진 점은 이상치로 간주되어 수염의 끝에서 부터 그리게 된다.
이상치 (Outliers): 수염 밖에 있는 개별 데이터 포인트들로, 주로 극단적인 값이나 측정 오류 등을 나타낸다.
중앙값 (Median): 상자 내부의 가로선으로, 데이터의 중앙에 있는 값을 나타낸다. 이것은 데이터의 중심 경향성을 보여준다.

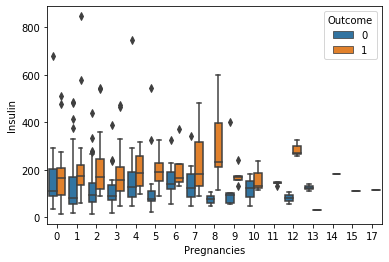
ⓛ 임신횟수(Pregnancies)에 따른 인슐린 수치(Insulin)를 당뇨병 발병여부(Outcome)에 따라 시각화

# 인슐린 수치에는 결측치가 많기 때문에 0보다 큰 값에 대해서만 그림

sns.boxplot(data=df[df["Insulin"] > 0],
            x="Pregnancies", y="Insulin", hue="Outcome")

3) violinplot

이번에는 또 다른 플롯인 violinplot을 활용해 시각화 해보자. violinplot은 boxplot과 유사한 정보를 제공하지만 더 많은 정보를 담고 있다. 바이올린 형태의 곡선을 가지고 있으며 그래프의 요소들은 다음과 같다.

바이올린 형태의 곡선: 각 값의 확률 밀도를 나타내는 곡선으로 데이터의 분포를 쉽게 이해할 수 있도록 도와준다. 곡선의 너비는 해당 값들의 밀도를 나타내며, 더 넓은 부분은 더 많은 데이터가 해당 영역에 분포되어 있음을 나타낸다.
중앙 표시 선: 바이올린 곡선 위에 있는 선은 중앙값(median)을 나타낸다.
상자 그림: 바이올린 곡선 내부에 있는 상자 그림은 데이터의 사분위수를 나타낸다. 상자 그림의 위와 아래 선분은 제 1 사분위수(Q1)와 제 3 사분위수(Q3)를 나타내고, 상자 내부의 가로선은 중앙값을 나타낸다.
이상치 (Outliers): boxplot과 유사하게, 바이올린 플롯에는 이상치도 표시된다.

# 인슐린 수치에는 결측치가 많기 때문에 0보다 큰 값에 대해서만 그림
# split=True로 설정하여 바이올린 플롯을 분할

plt.figure(figsize=(15, 4))
sns.violinplot(data=df[df["Insulin"] > 0],
            x="Pregnancies", y="Insulin", hue="Outcome", split=True)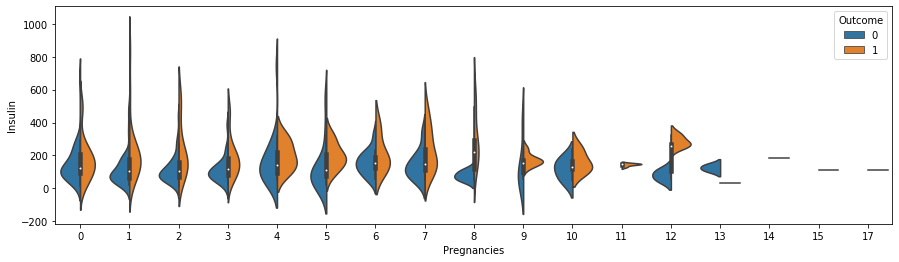

4) swarmplot (산포도)

다음으로는 swarmplot을 활용해보자. swarmplot은 데이터를 이산적인 점으로 표시하여 범주형 변수에 대한 연속형 변수의 분포를 시각화하는 데 사용되는 그래픽 기법 중 하나다. 각각의 데이터 포인트는 겹치지 않도록 살짝 이동된 위치에 표시되어 중복을 피하고 데이터의 분포를 잘 보여준다.

Swarmplot의 주요 특징은 다음과 같다:

이산적인 위치: 각 데이터 포인트는 이산적인 위치에 표시된다. 이는 데이터 포인트가 겹치지 않도록 만들어주어 중복을 피하고 데이터의 분포를 명확하게 시각화할 수 있도록 도와준다.
범주형 변수에 대한 연속형 변수의 분포: 주로 범주형 변수를 x축으로, 연속형 변수를 y축으로 사용하여 해당 범주에 속하는 데이터의 분포를 시각화한다.
점의 밀도: 데이터 포인트들이 얼마나 밀집되어 있는지를 시각적으로 확인할 수 있다. 더 밀집한 지역에는 더 많은 데이터 포인트가 있음을 의미한다.
이상치 확인: 이상치나 극단값을 시각적으로 확인할 수 있다. 이상치는 주로 범주형 변수에 대한 연속형 변수의 극단적인 값을 나타낸다.

위의 그래프를 swarmplot으로 시각화하는 것은 다음과 같다.

plt.figure(figsize=(15, 4))
sns.swarmplot(data=df[df["Insulin"] > 0],
            x="Pregnancies", y="Insulin", hue="Outcome")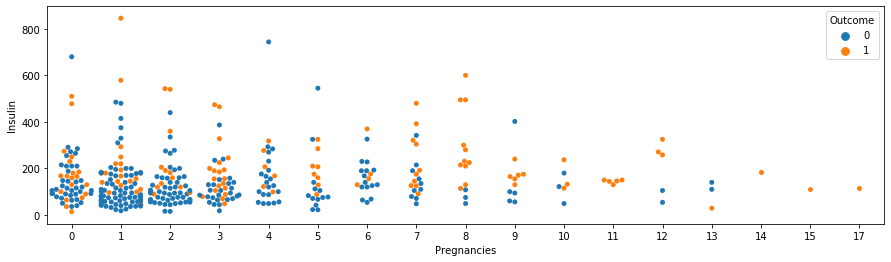

2.1.5 수치형 변수의 분포를 정답값에 따라 시각화 해보기

● distplot() 의 이해

seaborn 라이브러리에 있는 distplot() 함수는 연속된 수치형 데이터를 시각화 하는데 사용된다. 앞에 Countplot은 data 옵션이 있었지만, 이 함수는 data 옵션 없이 바로 Series 데이터를 넣어준다.

형식: sns.displot(Series 형태 데이터, rug=..,bins=..)

■ bins: 히스토그램의 구간(bin)의 수를 결정한다. 사용자 지정이 가능하다.
■ rug: 각 관측치를 러그(rug) 플롯으로 나타낼지 여부를 결정한다. 기본값은 False이다.
이외에도 다양한 옵션들이 있다 !!

※ Countplot: 범주형(카테고리형) 데이터를 시각화 할때 사용한다.

● 임신 횟수에 따른 당뇨병 발병 여부를 시각화해보자 [실습]

1. 당뇨병 여부에 따라 df를 df_0과 df_1로 나눠준다.

#Outcome이 0일때 df_0
df_0=df[df['Outcome']==0]

#Outcome이 1일때 df_1
df_1=df[df['Outcome']==1]

df_0은 Outcome이 0일 때의 데이터를 분리시킨거고 df_1은 Outcome이 1일 때의 데이터를 다룬것이다.

2. seaborn의 distplot으로 그래프를 그려준다.
(추가로 rug 옵션을 설정해주었다)

#임신 횟수에 따른 당뇨병 발병 여부를 시각화한다
#당뇨병이 일어났다고 했을때 그때 임신 횟수들의 빈도를 구해줌
#당뇨병이 일어나지 않았을때 임신 회수들의 빈도를 구해줌
#판다스 시리즈를 넣어준다

sns.distplot(df_0['Pregnancies'],rug=True)
sns.distplot(df_1['Pregnancies'],rug=True)

rug옵션을 택하면, 마치 카페트의 끝처리처럼 그래프를 그려준다.
3. 결과를 분석해보자

주황색 영역은 Pregnancies(임신횟수)가 1일때, 파란색 영역은 Pregnancies(임신횟수)가 0일때 이다.
파란색 밀도 그래프와 주황색 밀도 그래프는 값이 5일때 정도 교차한다. 그 이후는 주황색 밀도 그래프가 파란색 밀도 그래프를 추월한다. 이로써, 임신 여부가 5를 넘어가면 당뇨병 발병률이 더 높아짐을 알 수 있다.

●나이에 따른 당뇨병 발병 여부를 시각화 [실습]

1. 위에 정의했던 df_0,df_1 을 가지고 그려보자
(단, hist=False : 히스토그램은 제외하고 보자, 범례도 추가해주자)

#나이에 따른 당뇨병 발병 여부를 시각화 한다
#옵션: hist=False => 히스토그램 제외하고 보기
#label: 범례 제목 달아주기
sns.distplot(df_0['Age'],hist=False,label='0') #당뇨병이 발병한 케이스
sns.distplot(df_1['Age'],hist=False,label='1') #당뇨병이 발병하지 않은 케이스

■ hist=False를 하여 히스토그램을 제외하고 밀도 추정 곡선만 화면에 나타냈다.
■ label 옵션을 적용하여 범례를 추가해줄수 있다. 범례는 0,1로 각각 할것이다.

3. 결과 분석
30대 이후에는 당뇨병 발병 케이스가 더 많음을 확인 가능하다.
히스토그램을 제외하고 밀도 추정 곡선만 그리니까, 차이를 더 뚜렷하게 비교 할수 있는 것 같다.

2.1.6 서브플롯으로 모든 변수 한번에 시각화하기

● subplot ()의 이해

subplot은 플롯을 여러 개의 작은 영역으로 분할하여 여러 개의 Grid를 만드는 것을 의미한다. 이를 통해 하나의 그림 영역에 여러 개의 서로 다른 플롯을 배열할 수 있다.

다만, subplot만 그리면 빈 Grid 뿐이다. 이 빈 Grid에 그래프를 하나하나씩 다 그려줘야할까?
반복문을 사용하면, 위 작업을 간소화 시킬 수 있다.

● 반복문을 통해 displot 여러개 그리기

< 구성 >
1. subplot 옵션 정의해주기

#컬럼의 수만큼 for문을 만들어서 서브플롯으로 시각화하기
col_num=df.columns.shape
#Pregnancies_high 만 빼고 가져와서 그려보자
cols=df.columns[:-1].tolist()

fig,axes=plt.subplots(nrows=3,ncols=3,figsize=(15,15) )

■ nrows: Grid 행 수를 정의해준다.
■ ncols: Grid 열 수를 정의해준다.
EX) 4개의 그래프를 그리고 싶다면, 2 by 2 이므로, nrows=2, ncol2 로 설정해야한다.

그럼 fig와 axes에다가 왜 따로 변수로 저장해줘야할까?
subplot는 빈 Grid와 배열 객체를 반환한다. 따라서, fig는 빈그림이고, axes는 개체의 배열을 담고 있다.

< 원리 예시 >
EX) axes[0][0] 이라고 하면, Grid의 0행 0열에다가 그래프를 그리겠다는 뜻이다.

2. 반복문 작성해주기

for i,col_name in enumerate(cols):
 #인덱스 지정방법
  row=i//3 #3개씩 들어가니까,소수점 제외
  col=i%3 #나머지값으로
  print(i,col_name,row,col)
  sns.distplot(df[col_name],ax=axes[row][col])

■ enumerate: index값과 cols를 반환한다.
■ ax 옵션: axes 위치 값을 설정해준다.

row는 index에 따라 3으로 나눠지고 몫 값을 가져온다.
col은 index를 3으로 나눴을때 나머지를 사용한다.
위 같은 방식으로 적용하다 보면, 3 by 3 행렬에 00,01,02,10,11,12,20 위치값으로 그래프가 잘 들어간다.

3. 그래프 보기

다만, 위에서 적용한 실습은 Outcome 여부에 상관없이 각 열의 빈도수를 고려한것이다. 아래 실습에서 Outcome 값에 따라 displot을 그려보자.

● 반목문을 통해 Outcome 의 여부에 따라 distplot을 그려보기

Outcome 0,1여부에 따라 distplot을 그려보려고 한다. 위에서 정의한 df_0과 df_1을 다시 끌어온다.
<위 코드와 작동원리가 같으므로 코드 설명은 따로 하지 않겠다>

fig,axes=plt.subplots(nrows=4,ncols=2,figsize=(15,15) )
#모든 변수에 대한 displot을 그려봅시다
#outcome 값은 빼고 그리자


for i,col_name in enumerate(cols[:-1]):
 #인덱스 지정방법
  row=i//2 #2개씩 들어가니까,소수점 제외
  col=i%2
  print(i,col_name,row,col)
  #Outcome이 0인 것에 따라 그림
  sns.distplot(df_0[col_name],ax=axes[row][col])
  #Outcome이 1인것에 따라 그림
  sns.distplot(df_1[col_name],ax=axes[row][col])

<결과 분석>
1. Glucose 수치가 125이상이면 당뇨병이 더 잘 발병한다.
2. BMI 수치가 30을 넘어가면 당뇨병에 걸릴 확률이 높다.

위와 같이 Outcome 결과에 따른 그래프 교차점에 따라 결과를 다양하게 해석 할 수 있다.

2.1.7 시각화를 통한 변수 간의 차이 이해하기

violinplot으로 subplot 그리기

fig, axes = plt.subplots(nrows=4, ncols=2, figsize=(15, 15))

우선 위에서 설명한 바와 같이 subplot의 옵션을 설정한다.

for i, col_name in enumerate(cols[:-1]):                             
        row = i // 2
        col = i % 2
        print(i, col_name, row, col)
        sns.violinplot(data=df, x="Outcome", y=col_name, ax=axes[row][col])

enumerate() 을 통해 index 값과 cols를 차례대로 반환하고, ax 를 통해 axes 위치 값을 설정한다.

결과 :

regplot 으로 두 변수의 상관관계 시각화하기

우선 'Insulin 수치와 Glucose 수치는 Outcome(당뇨병 발병 여부)과 긴밀한 연관이 있을 것이다.' 라는 가설을 세운다.

가설을 증명하기 위해 Insulin과 Glucose를 Outcome으로 구분해보자.

sns.regplot(data=df, x="Glucose", y="Insulin")

단일 색상을 사용하는 regplot을 통해 Insulin과 Glucose의 상관관계를 분석한다.

결과 :

위의 차트는 가독성이 떨어지기에 구분되는 색상이 지원되는 lmplot을 통해 다시 그려본다.

sns.lmplot(data=df, x="Glucose", y="Insulin", hue="Outcome")

hue="Outcome" 을 통해 Outcome의 두 가지 경우를 다른 색상을 시각화했다.

결과 :

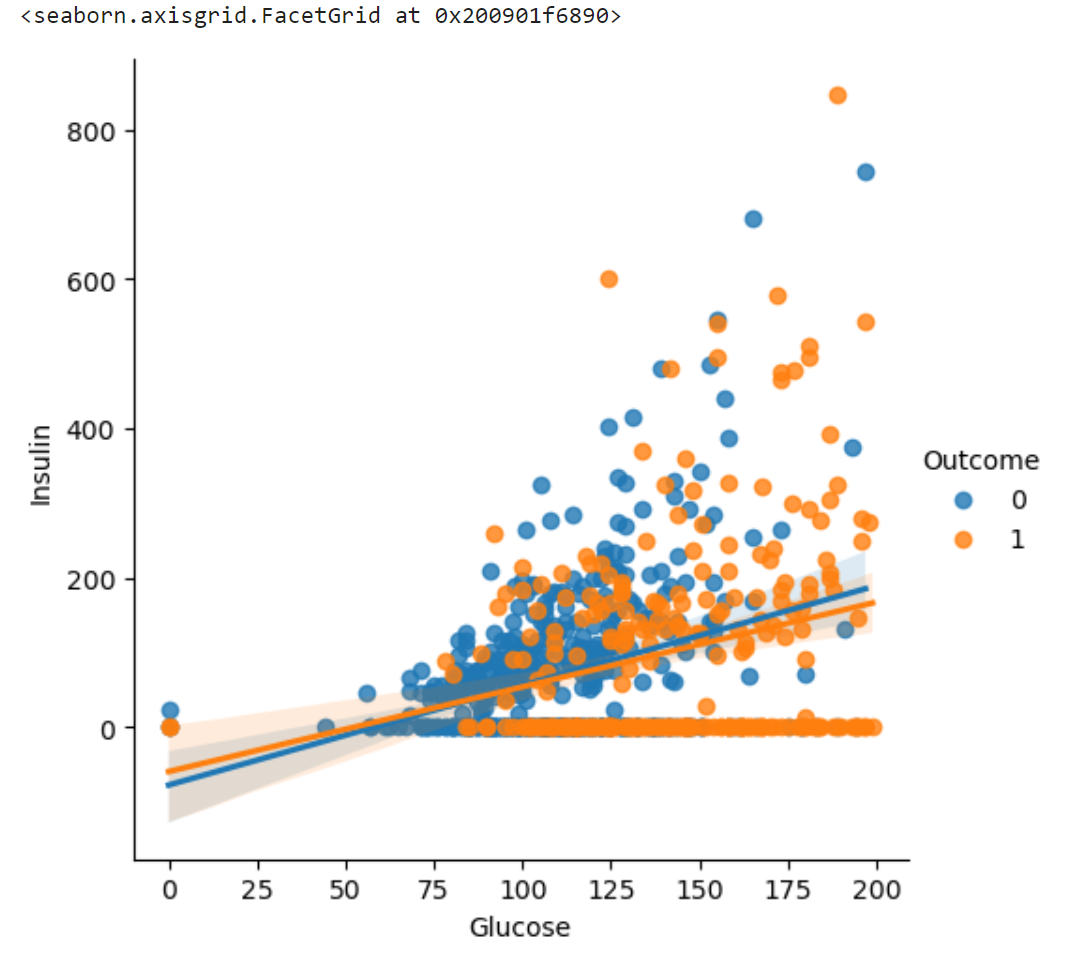
그러나 위의 차트는 Insulin 수치가 0인 데이터들을 포함하였다.

sns.lmplot(data=df[df["Insulin"] > 0], x="Glucose", y="Insulin", hue="Outcome")

인슐린 수치가 0인 데이터는 결측치로 간주해야 하므로 0 초과인 데이터들로만 시각화한다.

결과 :

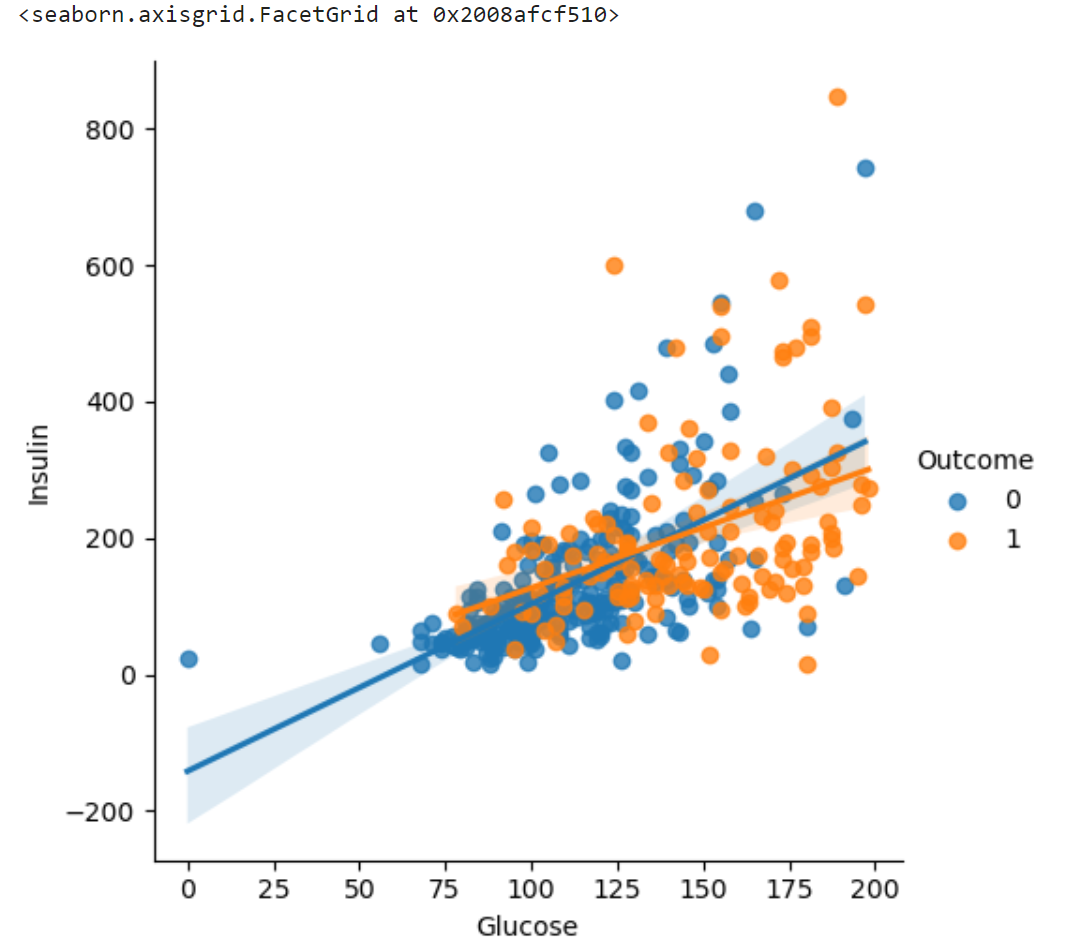
회귀선의 기울기가 1에 가까울수록 상관계수가 높은데, 인슐린 값이 0인 데이터를 제외하고 난 후의 상관계수가 높은 것을 파악할 수 있다.

pairplot을 통해 모든 변수 시각화하기

sns.pairplot(df)

seaborn 패키지에서 제공하는 pairplot을 통해 모든 변수(수치)를 시각화했다. 이때 결과는 scatterplot 형태로 반환된다.

결과 :

PairGrid를 통해 모든 변수 시각화하기

PairGrid를 통해 모든 변수를 Outcome에 따른 scatterplot으로 반환해보았다.

g = sns.PairGrid(df, hue="Outcome")
g.map(plt.scatter)

hue="Outcome" 을 통해 Outcome의 두 가지 경우를 다른 색상을 시각화하고,

map()을 통해 형태를 scatterplot으로 반환하였다.

결과 :

이처럼 pairplot 또는 PairGrid를 통해 변수들의 상관관계를 분석할 수 있다.

2.1.8 피처엔지니어링을 위한 상관 계수 분석하기

상관분석

상관분석이란 두 변수 간에 어떠한 선형적 관계를 갖고 있는 지를 분석하는 방법이다.

일반적으로

r이 -1.0과 -0.7 사이이면, 강한 음적 선형관계,

r이 -0.7과 -0.3 사이이면, 뚜렷한 음적 선형관계,

r이 -0.3과 -0.1 사이이면, 약한 음적 선형관계,

r이 -0.1과 +0.1 사이이면, 거의 무시될 수 있는 선형관계,

r이 +0.1과 +0.3 사이이면, 약한 양적 선형관계,

r이 +0.3과 +0.7 사이이면, 뚜렷한 양적 선형관계,

r이 +0.7과 +1.0 사이이면, 강한 양적 선형관계

로 해석된다.

df_corr = df.corr()
df_corr.style.background_gradient()

pandas에서는 상관관계 분석 툴을 제공한다. 우선 결측치(ex 인슐린 값 0)를 제거하지 않은 상태로 변수들의 상관관계를 구해보았다.

결과 :

위에서 구한 상관계수를 heatmap으로 시각화해보았다.

sns.heatmap(df_corr)

결과 :

위 heatmap은 음수는 모두 어두운 색으로 처리했다. (-)의 값도 구분하고 싶다면, 위의 코드에 vmax=1, vmin=-1 을 추가한다.

plt.figure(figsize = (12,7))
sns.heatmap(df_corr, annot=True, vmax=1, vmin=-1, cmap="coolwarm")

annot=True 를 통해 박스 안에 변수들의 상관계수를 적어주었다.

cmap="coolwarm"을 통해 음수일 때는 푸른 계열의 색상이 반환되게 하였다.

결과 :

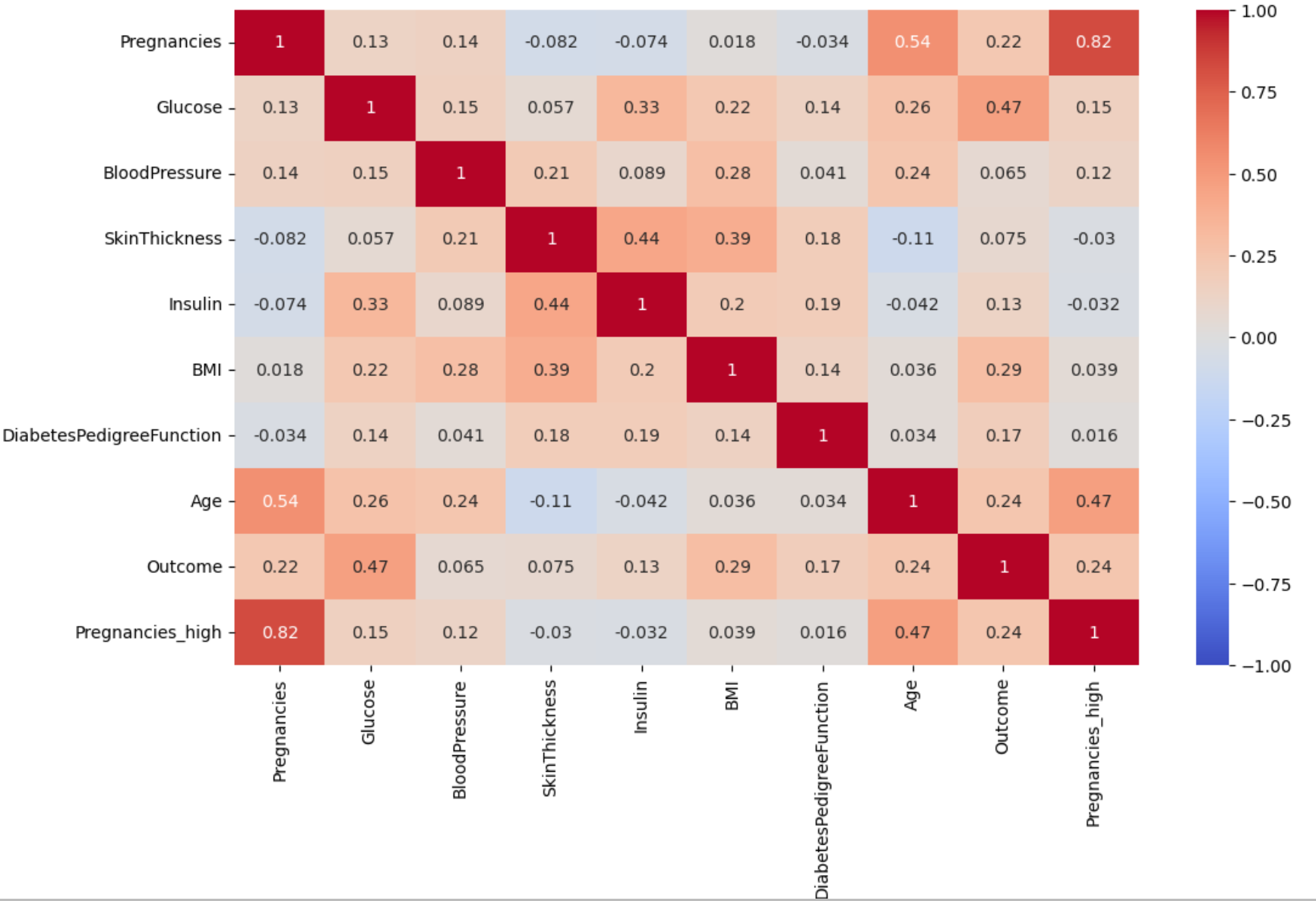
위에서 보다시피 Insulin 같은 변수의 경우 0, 즉 결측치로 간주해야 할 값이 많으므로 상관계수가 작은 모습이다. 따라서 0을 결측치로 만들어주는 작업을 수행해야 한다.

df_matrix = df.iloc[:,:-2].replace(0, np.nan)
df_matrix["Outcome"] = df["Outcome"]
df_matrix

우선 Pregnancies_high 와 Outcome 열을 제외한 dataframe에서 0을 결측치로 바꾸는 작업을 수행하였다. 그 후 Outcome 열을 추가한 df_matrix 를 만들어주었다.

결과 :

df_corr = df_matrix.corr()
plt.figure(figsize = (12,7))
sns.heatmap(df_corr, annot=True, vmax=1, vmin=-1, cmap="coolwarm")

0을 제외하지 않고 heatmap을 반환하는 코드와 똑같이 이번에는 df 대신에 df_matrix를 넣고 박스 안에 상관계수를 출력하는 heatmap을 만들어보았다.

결과 :

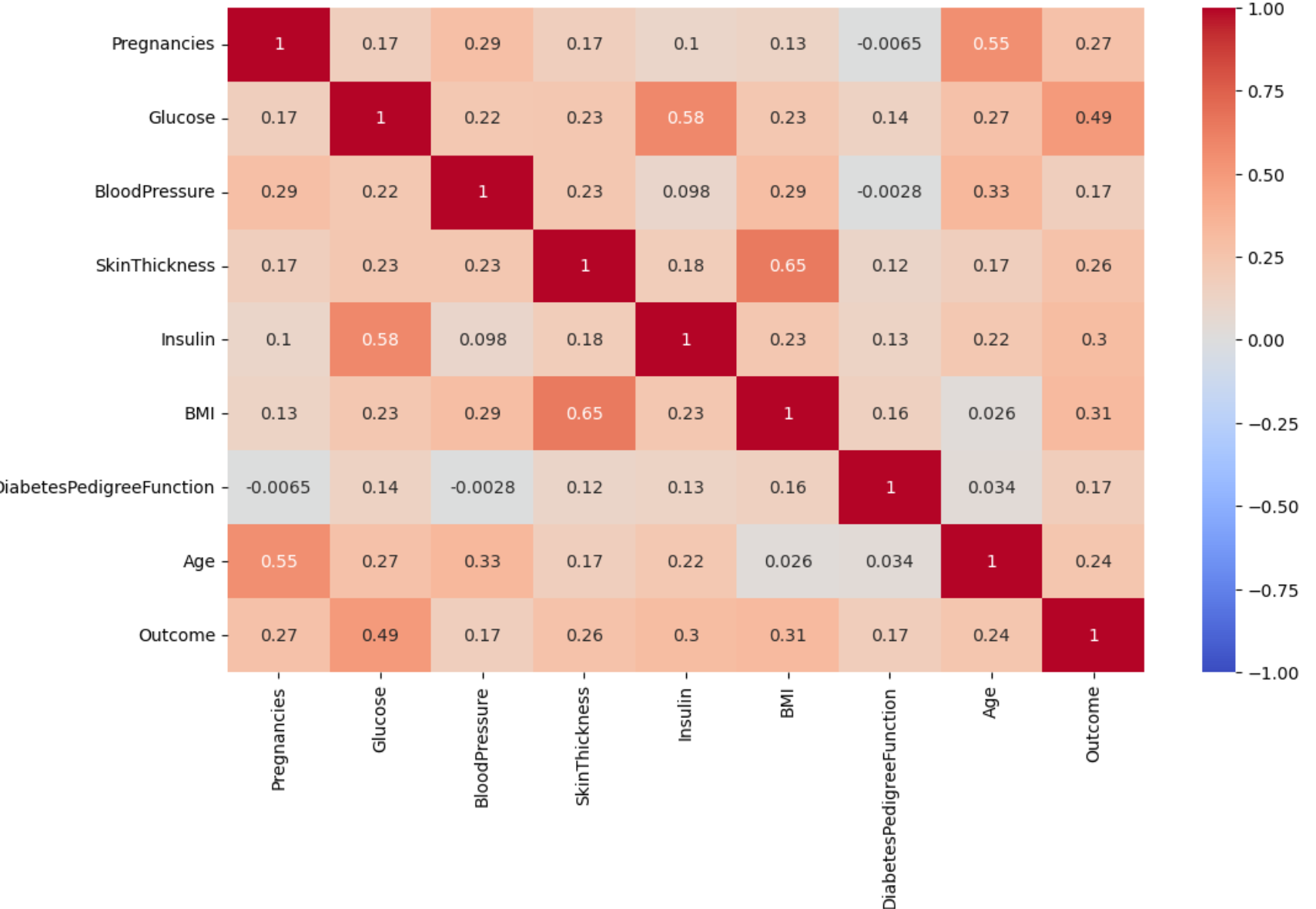
이로써 Insulin에 대한 Glucose와 Outcome의 상관계수가 높아진 결과를 출력하였다.

df_corr["Outcome"]

우리가 알고 싶은 것은 Outcome 수치에 대한 상관계수이므로 당뇨병 발병 여부 데이터와 관련한 상관계수만 모아서 반환하였다.

결과 :

위 정보를 바탕으로 Glucose 와 Insulin, BMI 가 Outcome과의 상관관계가 높은 것으로 결론을 냈다.

상관관계가 높은 변수끼리 보기

sns.regplot(data=df_matrix, x="Insulin", y="Glucose")

위의 heatmap에서 상관계수가 높았던 Insulin과 Glucose 수치로 regplot을 그려보았다.

결과 :

앞서 설명하였듯이 회귀선의 기울기가 1에 가까울수록 상관계수가 높은 것을 의미한다.

이 차트에서 주의하여 볼 것은 회귀선과 먼 이상치(outlier)들을 전처리 할 것인지 쓸 것인지 판단해야 한다는 점이다.

sns.lmplot(data=df, x="Age", y="Pregnancies", hue="Outcome", col="Outcome")

이번에는 Age 와 Pregnancies를 lmplot으로 그리고 hue를 통해 Outcome을 다른 색상으로 표시해보았다.

또한 col="Outcome" 을 통해 Outcome이 0과 1인 경우를 따로 분리하여 subplot으로 반환하였다.

결과 :

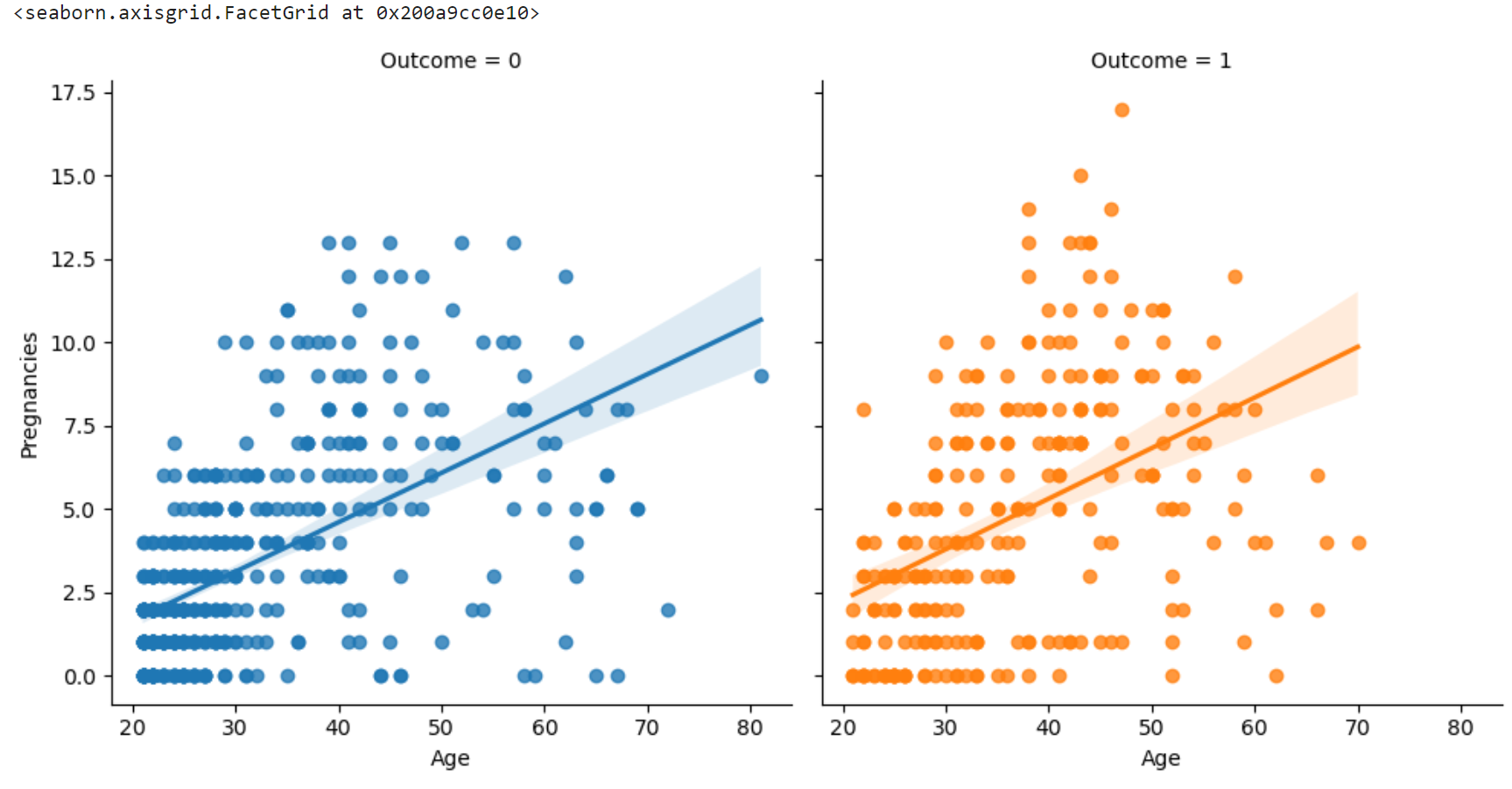
이처럼 EDA 데이터를 바탕으로 어떠한 변수를 어떻게 사용하면 좋을지 판단해야 한다. 예를 들면 결측치를 어떻게 처리할지, 이상치를 감안할지 처리할지 등을 판단하여 성능이 뛰어난 모델을 만드는 발판을 다져야 한다.

<2주차 과제>

2024_CODE_2기__프로젝트로_배우는_데이터사이언스__2주차_과제 (3).ipynb

1.36MB

저작자표시 비영리 동일조건