3.1 탐색한 데이터로 모델 성능 개선
3.1.1 연속 수치 데이터를 범주형 변수로 변경하기
이전에 1주차 내용에서 피처 엔지니어링과 전처리를 전혀 하지 않은 상태에서 데이터 셋을 나누어, DecisionTree ML 알고리즘을 통해서 예측을 진행 했습니다. 이때 71.43%의 정확도가 나왔었습니다.
이 정확도를 개선하는 방법들을 다음과 같습니다:
- feature engineering
- model의 parameter tuning (모델 성능 개선)
2번에 대한 설명을 간단히 하자면, 지난번의 예측에선 DecisionTreeModel의 기본 옵션만을 사용했지만,
- tree의 깊이 제한
- leaf node의 샘플 개수 조정
- node가 나뉘어 질 때 최소한의 샘플 개수 지정
이런 방법으로 모델의 성능을 개선해 볼 수 있습니다.
이번 내용에서는 Feature Engineering에 중점을 둘 것입니다.
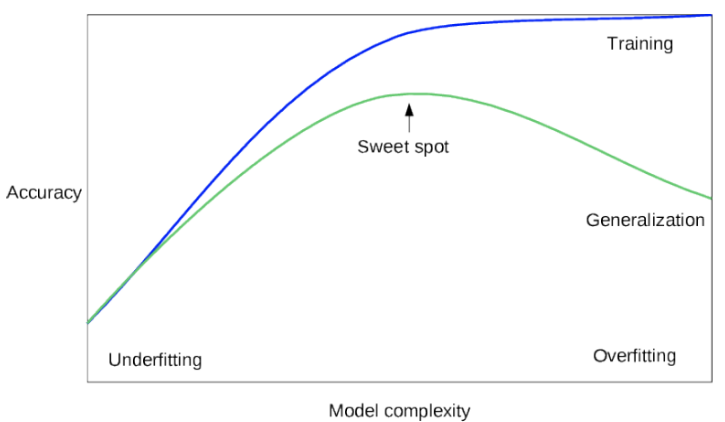
- Overfitting이란? -
Overfitting은 한국어로 "과적화"라고 불리며 모델이 학습 데이터에 학습을 너무 많이 하여 학습데이터에 대한 정확도는 높지만, 다른 샘플/데이터에 대한 정확도는 오히려 낮아지는 현상입니다.
기출문제를 정말 열심히 풀었는데 답도 다 외웠는데 막상 시험에 가니 다른 문제가 나와서 못 푸는 것이랑 비슷한 상황이라고 볼 수 있습니다.
- 그럼 우리 데이터도? -
지난번에 시각화한 histogram들을 보면, pregnancy, glucose, age를 포함한 여러 수치들이 당뇨병의 발병 여부에 따라 다른 분포도를 보여주고 있습니다.
여기서 Age, Insulin, 그리고 SkinThickness 같은 항목들은 수치의 범위가 꽤 넓은 편입니다. 이렇게 범위가 넓은 수치형 변수들은 DecisionTreeModel에서 조건이 엄청 세분화 되어 나눠지게 됩니다. (leaf 샘플의 개수가 1개, 2개가 생기는 경우가 발생)
이렇게 수치형 변수가 잘게 나뉘어지고, 그렇게 나뉘어진 샘플의 개수가 적은 세부항목의 데이터로 학습을 하면 trainig dataset에 overfitting(과적화) 현상이 발생하기 쉽습니다. 그러므로 연속형 수치 데이터를 범주형 데이터로 만들어 주어서 overfitting을 방지하기도 합니다.
- 피마 인디언 당뇨병 데이터를 이용한 전처리 실습 -
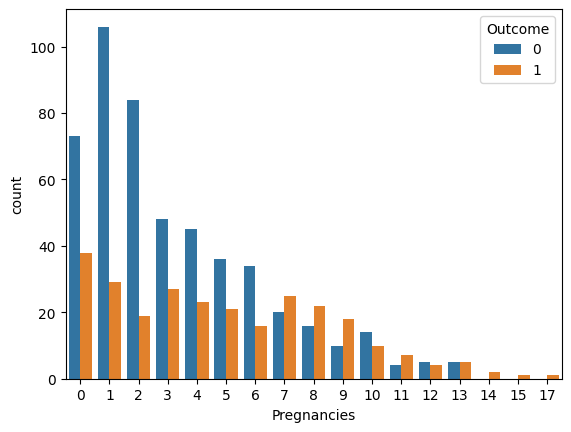
2주차에 진행했던 시각화를 보면, 우측 하단에 높은 임신횟수엔 샘플 사이즈가 훨씬 적은 것을 볼 수 있습니다.
이런 샘플들에 대한 과적화를 방지하기 위해 Pregnancies 수치형 변수를 범주형 변수로 만들겠습니다. 그 후에 범주형 변수 Pregnancies_high를 적용시켜 DecisionTreeModel을 학습 및 예측해 보겠습니다.
# Pregnancies가 6보다 높을 경우 Pregnancies_high로 정의
df['Pregnancies_high'] = df['Pregnancies'] > 6- 데이터 학습 및 예측 파이프라인 -
이번 장에 전처리를 다르게 한 데이터를 가지고 학습 및 예측을 실시할 예정인데 그 파이프라인을 한번에 정리해서 여기다 명시하겠습니다:
1. 학습 / 예측 데이터셋 나누기
# 학습, 예측 데이터셋 나누기 (8:2)
split_count = int(0.8*df.shape[0])
# 학습 데이터셋 지정
train = df[:split_count].copy()
# 예측 데이터셋 지정
test = df[split_count:].copy()2. 학습 / 예측에 사용할 컬럼 분류
# 학습에 사용할 항목들을 별도로 분류합니다.
feature_names = train.columns.tolist()
# Pregnancies_high로 Pregnancies 항목을 대체합니다.
feature_names.remove("Pregnancies")
feature_names.remove("Outcome")
feature_names['Glucose',
'BloodPressure',
'SkinThickness',
'Insulin',
'BMI',
'DiabetesPedigreeFunction',
'Age',
'Pregnancies_high']
# 예측값 컬럼을 지정합니다.
label_name = "Outcome"3. 학습 / 예측 항목 분류
# 학습 데이터셋을 만듭니다.
X_train = train[feature_names]
y_train = train[label_name]
# feature들이 제대로 들어있는지 확인합니다.
X_train.head()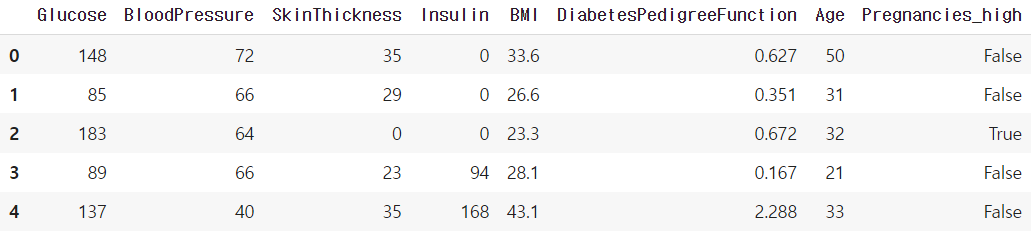
Pregnancies 컬럼이 제외되었고 대신 Pregnancies_high 컬럼이 사용되는 것을 볼 수 있습니다. Pregnancies_high의 dtype이 boolean인 것도 확인이 됩니다. 비록 데이터타입이 int나 float이 아니지만, DecisionTreeModel이 False는 0, True는 1로 인식하기 때문에 학습에 문제가 되지 않습니다.
# 동일하게 예측 데이터셋도 만들어 줍니다.
X_test = test[feature_names]
y_test = test[label_name]4. 의사결정나무 모델 불러오기
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier()5. 모델 학습 및 예측 실행
# 학습과정 진행
model.fit(X_train,y_train)
# 예측
y_predict = model.predict(X_test)- 학습된 모델 시각화 및 분석 -
1. 트리 시각화
from sklearn.tree import plot_tree
plt.figure(figsize=(20,20))
tree = plot_tree(model, feature_names=feature_names, filled=True, fontsize=10)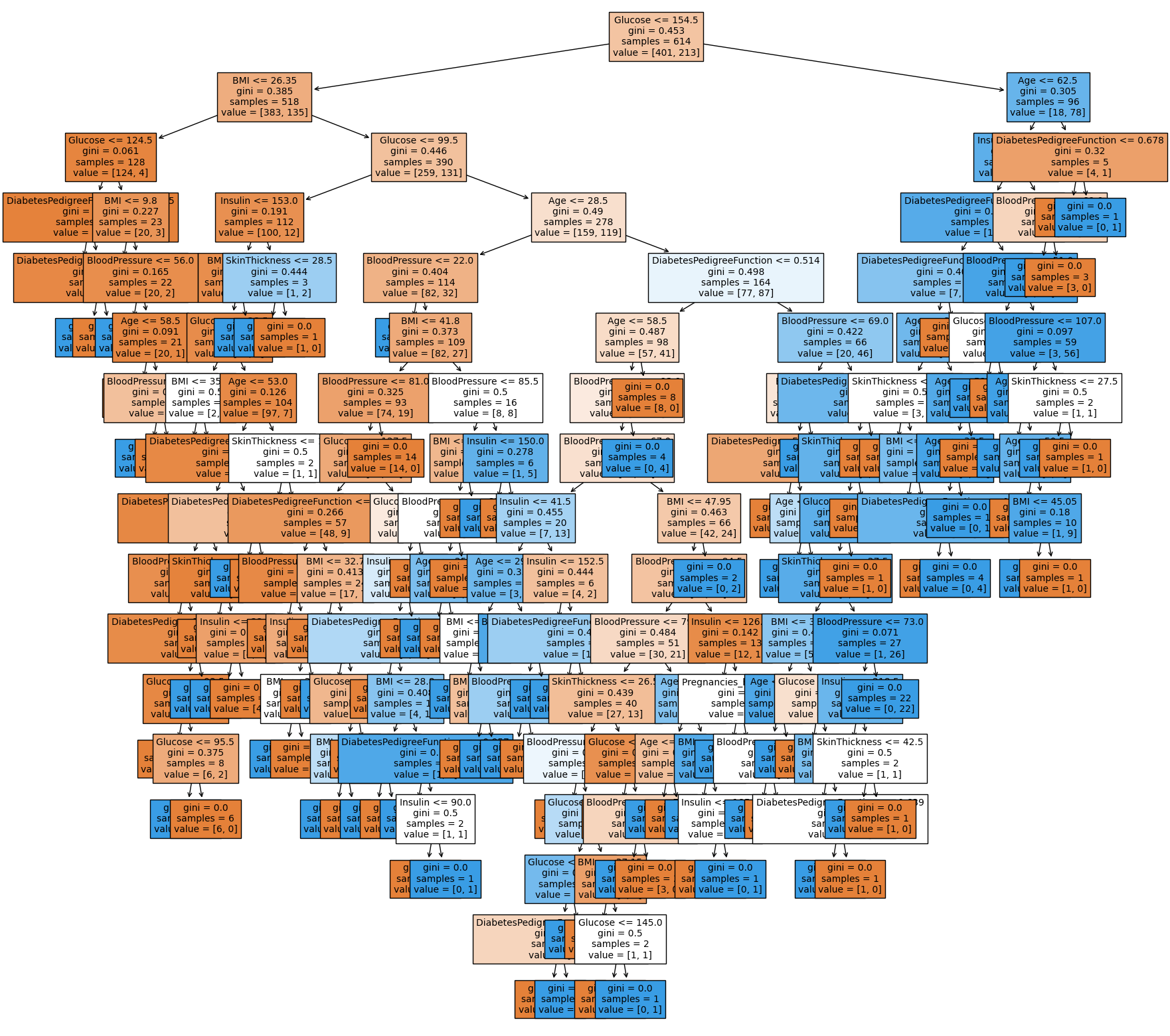
1주차 때 시각화 했던 트리와 거의 비슷하게 그려졌습니다. 여전히 Glucose가 첫번째 branch로 가장 중요한 역할을 하고 있는 것을 볼 수 있습니다.
2. 피처 중요도 시각화
# feature_importance 수치를 보겠습니다.
model.feature_importances_
# feature_importance 시각화 하기
sns.barplot(x=model.feature_importances_,y=feature_names, hue=feature_names)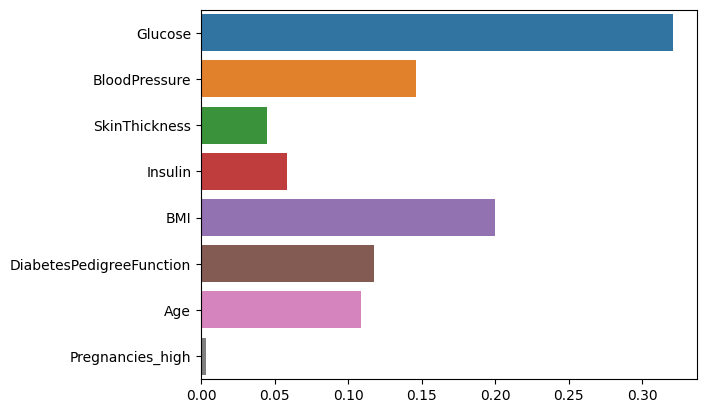
1주차의 그래프랑 비교했을때, Pregnancy의 중요도 보다 Pregnancies_high의 중요도(가장 아래)가 훨씬 낮게 나온것을 볼 수 있습니다. 이번에 학습된 모델에서 Pregnancies_high는 별로 중요한 역할을 하지 않은 걸로 볼 수 있습니다.
3. 정확도 측정하기
# 실제 답과 예측값이 얼마나 차이가 나는지 구합니다.
diff_count = abs(y_predict - y_test).sum()
# 예측의 정확도를 구합니다.
acc = (1 - diff_count/len(Y_test))*100
print(f"틀린 개수는 {diff_count}개, 정확도는 {acc}입니다.")틀린 개수는 34개, 정확도는 77.92207792207793으로 이전보다 올라간 것을 볼 수 있습니다.
3.1.2 범주형 변수를 수치형 변수로 변환하기 - 원핫인코딩
- Age 범주화 하기 -
이번엔 나이 항목을 범주화 하여 데이터를 학습해 보겠습니다.
Age 항목의 범주를 <25, 25~60, <60 세가지 분류로 나누어 주겠습니다.
df["Age_low"] = df["Age"] < 25
df["Age_middle"] = (df["Age"] >= 25) & (df["Age"] <= 60) # and 대신 & 사용!
df["Age_high"] = df["Age"] > 60이렇게 나이라는 수치형 변수를 각각 하나의 컬럼에 저장하며 각 항목에 해당하는 샘플은 True 값, 해당하지 않는 샘플엔 False 값을 입력해주었습니다.
이렇게 범주별로 나누어준 데이터를 각 범주 별로 시각화 해주겠습니다.
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 6))
sns.countplot(data=df, x="Age_low", hue="Outcome", ax=axes[0])
sns.countplot(data=df, x="Age_middle", hue="Outcome", ax=axes[1])
sns.countplot(data=df, x="Age_high", hue="Outcome", ax=axes[2])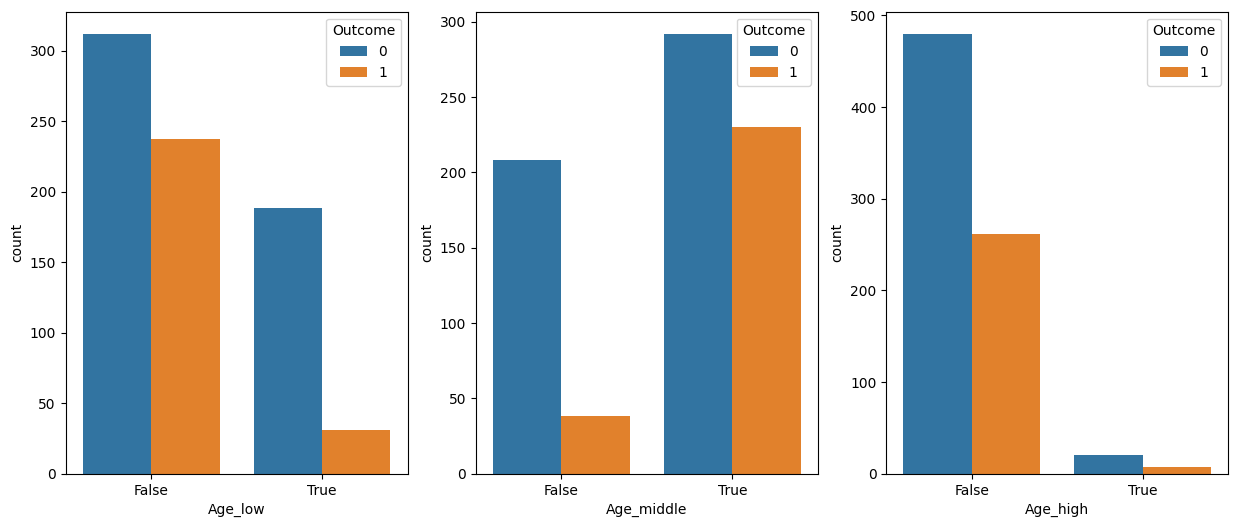
확실히 Age_low에 속해있는 샘플들은 발병률이 낮은 것을 볼 수 있습니다.
Age_middle에 있는 샘플들은 건강한 샘플들과 발병한 샘플들의 개수의 차이가 크지 않습니다.
Age_high에선 발병하지 않은 케이스가 발병한 케이스가 많지만 전체적으로 모수가 적습니다.
- 데이터 학습 및 예측 파이프라인 -
1. 3. 4. 5.동일
2. 학습 / 예측에 사용할 컬럼 분류
# 학습에 사용할 항목들을 별도로 분류합니다.
feature_names = train.columns.tolist()
# Pregnancies_high로 Pregnancies 항목을 대체합니다.
feature_names.remove("Pregnancies")
feature_names.remove("Outcome")
feature_names['Glucose',
'BloodPressure',
'SkinThickness',
'Insulin',
'BMI',
'DiabetesPedigreeFunction',
'Pregnancies_high',
'Age_low',
'Age_middle',
'Age_high']- 학습된 모델 시각화 및 분석 -
1. 트리 시각화
from sklearn.tree import plot_tree
plt.figure(figsize=(20,20))
tree = plot_tree(model, feature_names=feature_names, filled=True, fontsize=10)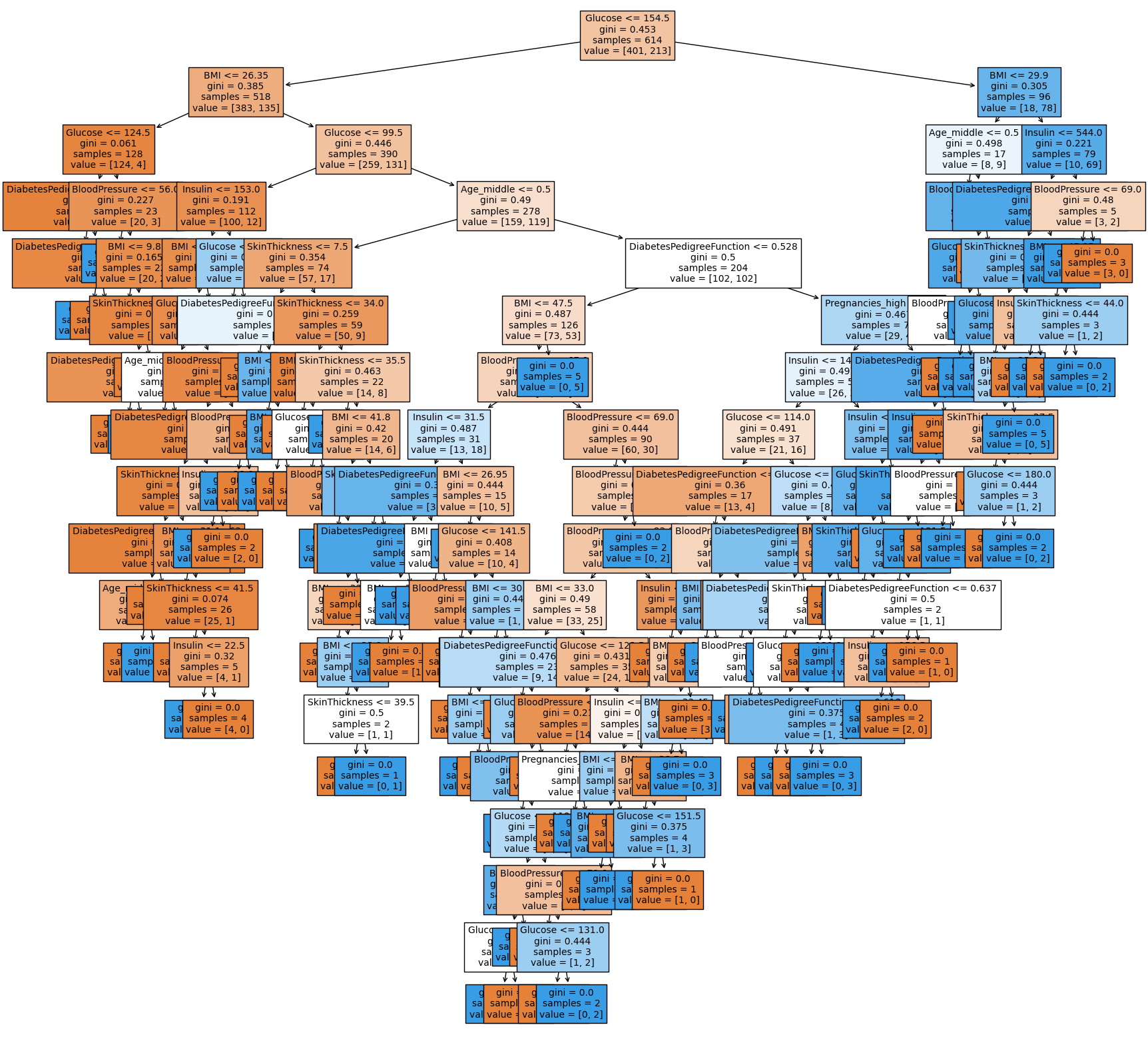
위에 시각화한 트리와 거의 비슷하게 그려졌습니다. 여전히 Glucose가 root node에 위치하면서 가장 중요한 역할을 하고 있는 것을 볼 수 있습니다.
2. 피처 중요도 시각화
# feature_importance 수치를 보겠습니다.
model.feature_importances_
# feature_importance 시각화 하기
sns.barplot(x=model.feature_importances_,y=feature_names, hue=feature_names)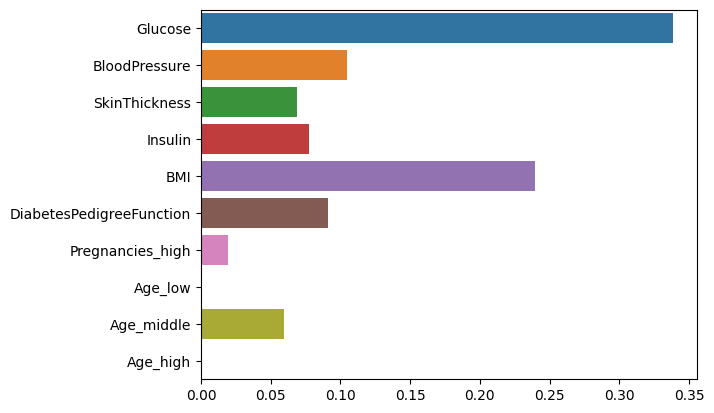
Age_low와 Age_high는 그렇게 큰 역할은 하지 않는 것처럼 보입니다. 그에 비해 Age_middle은 나름 모델의 예측에 영향을 미치는 항목이란 것을 볼 수 있습니다.
3. 정확도 측정하기
# 실제 답과 예측값이 얼마나 차이가 나는지 구합니다.
diff_count = abs(y_predict - y_test).sum()
# 예측의 정확도를 구합니다.
acc = (1 - diff_count/len(Y_test))*100
print(f"틀린 개수는 {diff_count}개, 정확도는 {acc}입니다.")틀린 개수는 50개, 정확도는 67.53246753246754로 이전보다 올라간 것을 볼 수 있습니다.
이번엔 실제 답과 예측값의 차이가 39개에서 50개로 오히려 늘어났습니다.
이렇게 전처리를 해줄 때 확연한 구분이 되지 않으면 오히려 정확도가 떨어질 수도 있습니다.
전처리시 다양한 기법들을 쓰는데, 모든 기법들이 모델의 성능을 올려준다는 보장은 없습니다.
이번에 저희가 해준 Age의 범주화는 성능을 올려주진 못했습니다.
이렇듯,범주화를 할 시에는 모델에 적용을 해보고 다양한 방법으로 시도를 하며 모델의 성능을 올리는 방법들을 찾는 것이 중요합니다.
3.1.3 결측치 평균값으로 대체하기
먼저 결측치를 봐야 한다.
df.isnull()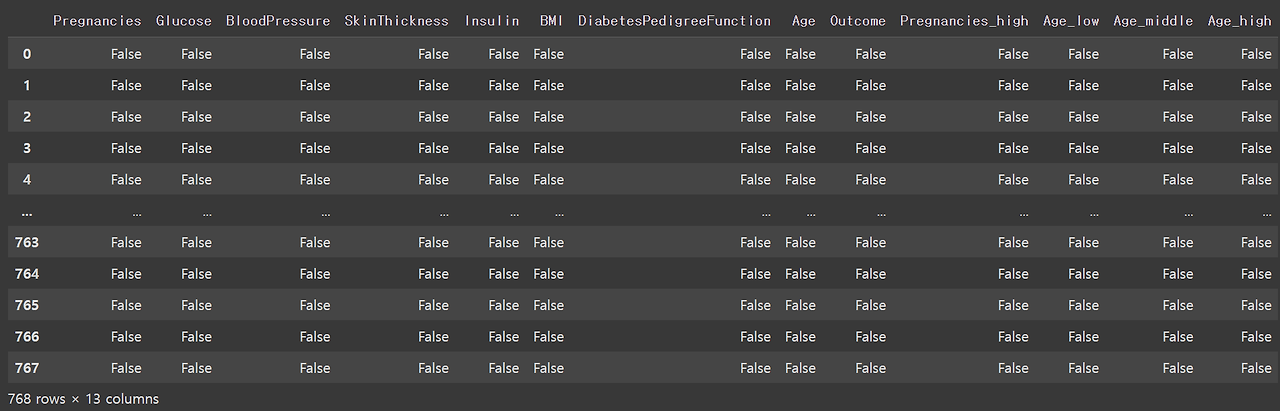
하지만 아무런 결측치가 없으므로 sum() 까지 사용한다.
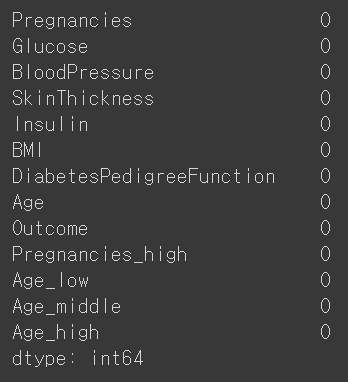
하지만 우리가 이 데이터를 요약했을 때,
df.describe()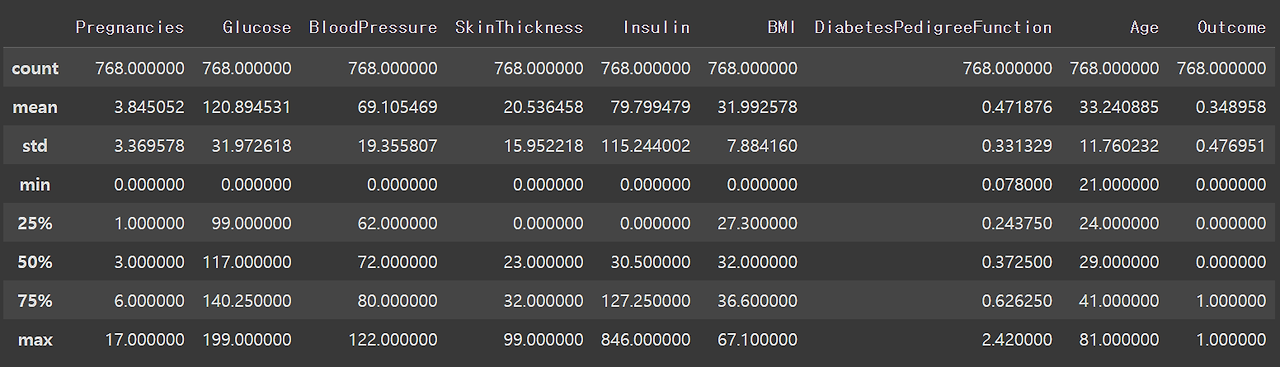
다음과 같은 결과에서 'Glucose', 'BloodPressure', 'SkinThickness', 'Insulin', 'BMI' 와 같이 최솟값이 0이 될 수 없는데 0이 들어가는 항목들이 존재한다.
우선, 인슐린을 가져오는데, 인슐린이 0보다 큰 값과 0보다 작은 값을 시각화 했을 때 Outcome 값과 확연히 구분되는 값들이 존재하기 때문에 예측을 하기 위해 0인 값을 고려해야 한다. 따라서 0 이 들어가는 값을 np.nan 을 사용해 NaN으로 바꿔준다.
df["Insulin_nan"]=df["Insulin"].replace(0,np.nan)
df["Insulin_nan"]
Insulin과 Insulin_nan의 상위 5개 컬럼만 확인해보자.
df["Insulin_nan"]=df["Insulin"].replace(0,np.nan)
df[["Insulin","Insulin_nan"]].head()
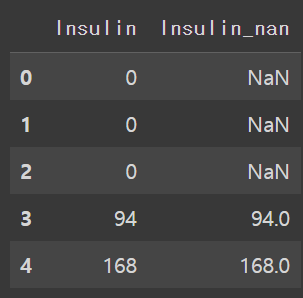
Insulin_nan에 isnull().sum() 을 사용해 총 결측치를 확인해보자.
df["Insulin_nan"].isnull().sum()
했을 때 결과가 "374" 가 나오는데, 이는 결측치가 374개 있다는 뜻이다.
mean()을 통해 결측치의 비율도 확인해보자.
df["Insulin_nan"].isnull().mean()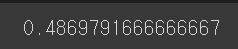
결측치의 비율이 48%나 된다..
결측치를 처리한 데이터와 처리하지 않은 데이터의 평균값이 어떻게 차이가 나는지 확인해보자.
df.groupby(["Outcome"])["Insulin","Insulin_nan"].mean()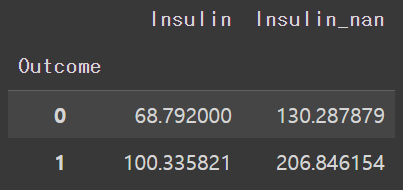
Outcome이 0일 때와 1일 때의 Insulin과 Insulin_nan의 결측치 데이터 모두 차이가 크게 나오는 것을 알 수 있다.
결측치가 너무 많으면 학습을 할 떄 오류가 발생할 확률이 증가한다.
결측치를 그대로 놔둔 채 학습을 진행해보자.
~이하 생략~
remove()를 사용해Insulin 값을 지워서 Insulin_nan 값만 남게 해주자.
feature_names=train.columns.tolist()
feature_names.remove("Pregnancies")
feature_names.remove("Outcome")
feature_names.remove("Insulin")
feature_names

이후 학습을 돌리면..
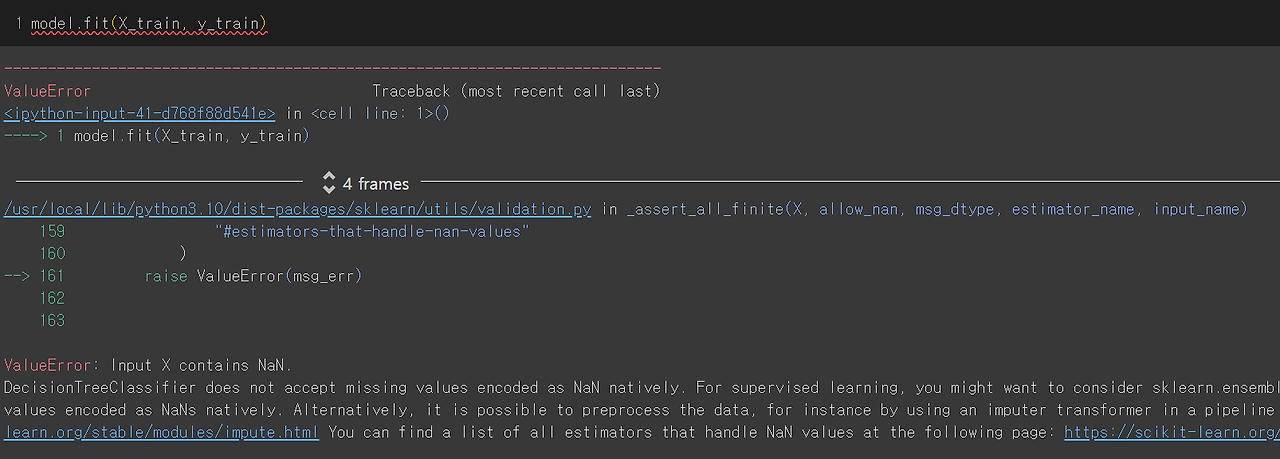
결측치를 포함했기 때문에 value error가 뜬다. 그러므로 결측치를 채워야 한다.
우선 agg() 함수를 통해 Insulin과 Insulin_nan 에서 mean 값과 median값만 따로 보자.
df.groupby(["Outcome"])["Insulin","Insulin_nan"].agg(["mean","median"])
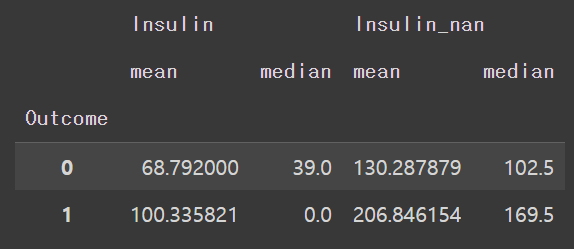
차이가 쫌 많이 나는 것을 알 수 있다.
이제 결측치를 채워보겠다.
Outcome의 값이 0일 경우엔 결측치인 130을, 1일 경우엔 206을 넣어줘 결측치를 없애보자.
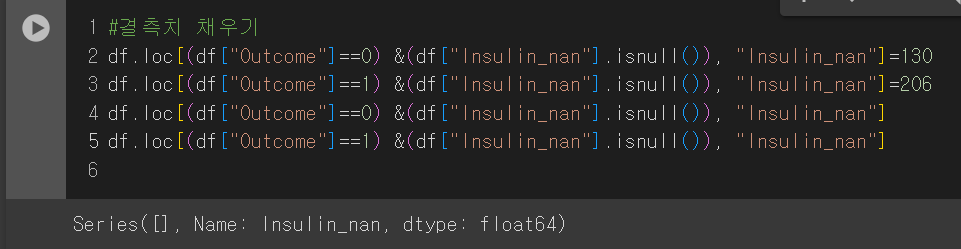
Insulin_nan이 isnull()인 값에 각각의 결측치를 삽입하면 다음과 같이 결측치가 없어짐을 알 수 있다.
이제 다시 학습을 돌려보자.
그리고 feature에서 정확도가 낮았던 Age_low, Age_middle, Age_high는 지워주겠다.
feature_names=train.columns.tolist()
feature_names.remove("Pregnancies")
feature_names.remove("Outcome")
feature_names.remove("Age_low")
feature_names.remove("Age_middle")
feature_names.remove("Age_high")
feature_names.remove("Insulin")
feature_names
계속해서 학습을 돌려보면 fit이 정상적으로 작동하는 것을 볼 수 있다.
이후 DecisionTree를 그려보면,
from sklearn.tree import plot_tree
plt.figure(figsize=(20,20))
tree=plot_tree(model,
feature_names=feature_names,
filled=True,
fontsize=10)
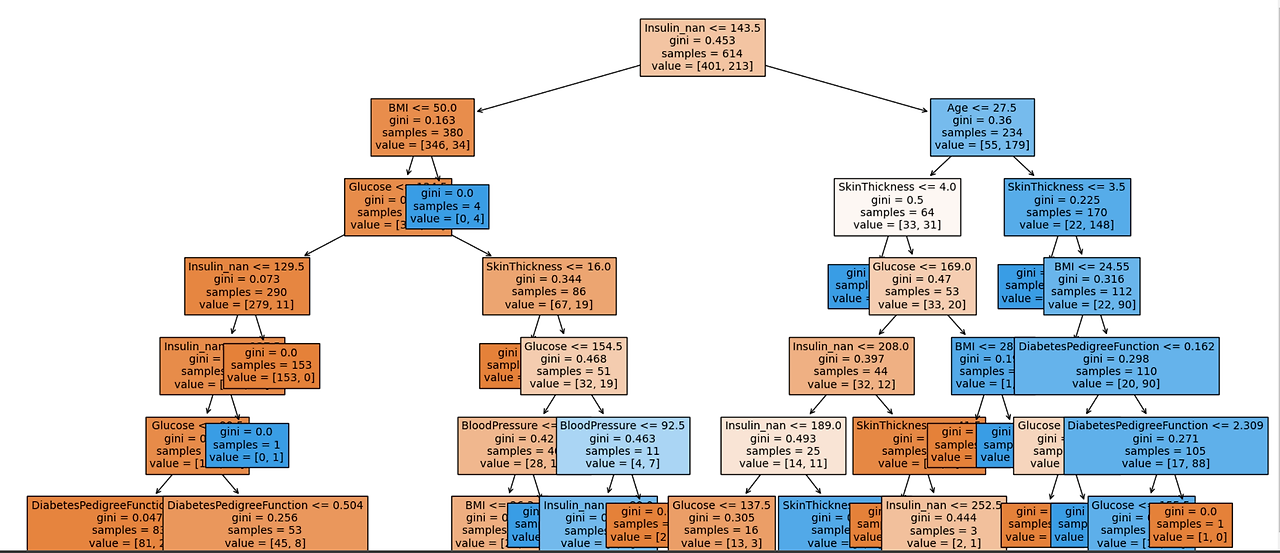
이전과 달리, 결측치를 채운 후 Insulin이 당뇨병 여부에 가장 중요한 역할을 함을 알 수 있다.
중요도를 시각화했을 때도 이전과 달리 인슐린 값이 가장 큰 역할을 함을 알 수 있다.
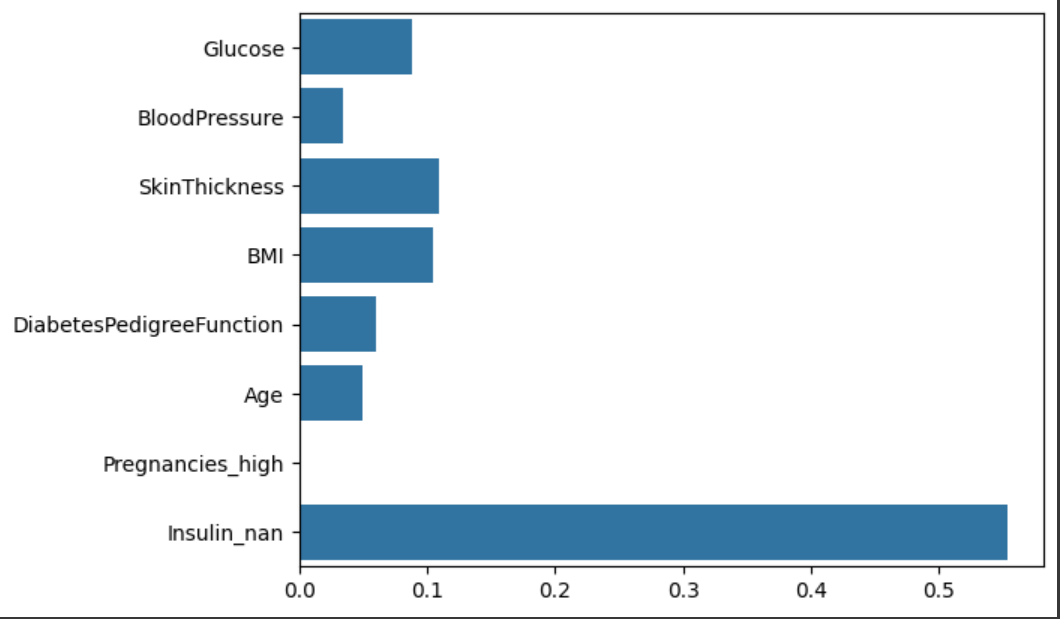
인슐린 결측치를 평균으로 대체한 값과 실제 정답값과의 차이를 구해보자.
diff_count = abs(y_test - y_predict).sum()
diff_count
값이 24가 나온다. 이는 앞서 나이를 기준으로 한 값에 비해 차이가 확연히 줄어듬을 알 수 있다.
예측 정확도를 비율로도 구해보자.

예측 정확도를 비율로 나타내보니, 다음과 같이 84%가 나왔다. 이는 이전보다 성능이 높아졌음을 알 수 있다.
3.1.4 결측치 중앙값으로 대체하기
이번엔 평균값이 아닌, 중앙값으로 대체했을 때 얼마나 증가하는 지 알아보겠다.
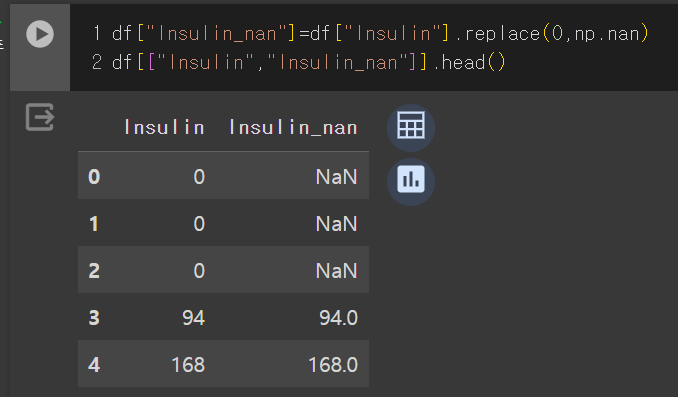
우선, 다시 원본 데이터 돌려 결측치를 만들어주었다.
~이하 생략~
이후 결측치에 중앙값인 102와 169를 넣어주도록 하겠다. 참고로 Outcome이 0인 경우에 102, 1인 경우에 169를 넣어주겠다.
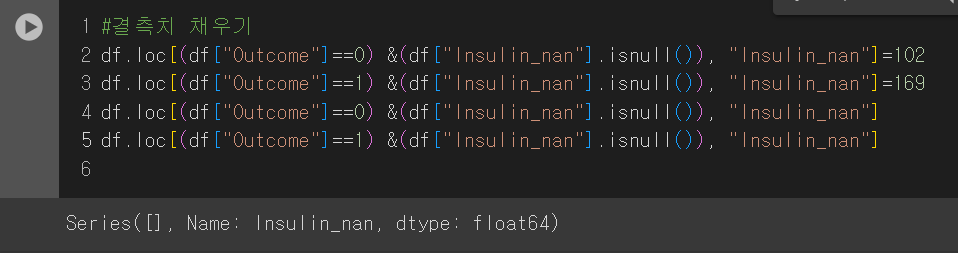
이후 머신러닝을 다시 돌려준다.
~이하 생략~
이후 DecisionTree 를 만들어주면,
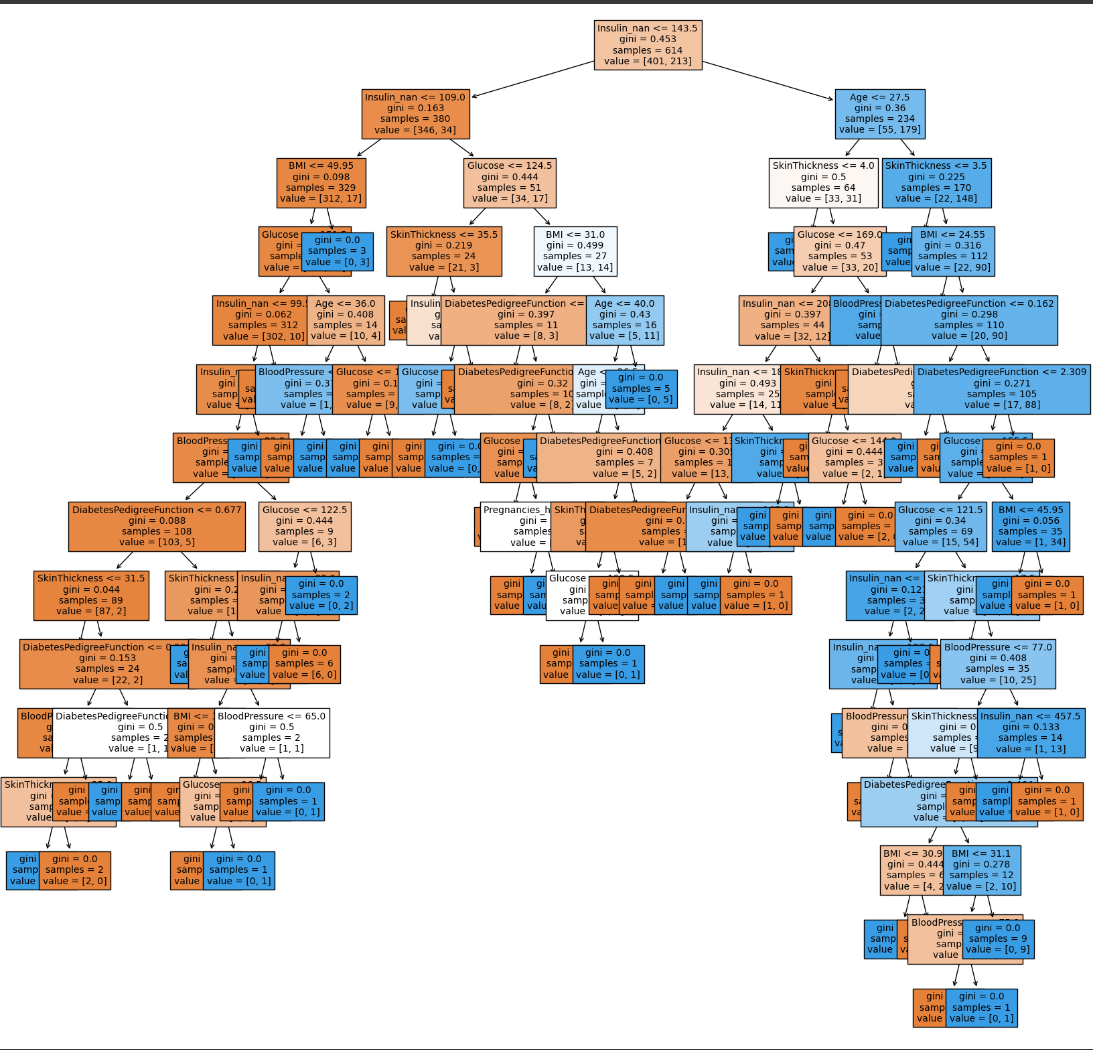
다음과 같이 의사결정나무가 만들어지며, 인슐린이 가장 중요함을 알 수 있다. 또한 나무가 아래로 깊게 내려옴을 알 수 있다. 또한 샘플이 적어지는데, 이는 오버피팅을 방지하기 위함이다.
이후 다시 정확도를 추출하면,
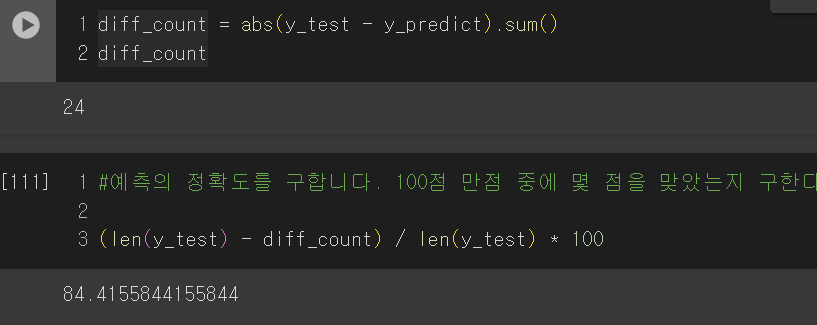
강의와 달리, 오차 범위가 줄어들지 않았으며, 정확도도 차이가 없다., 아무리 강의와 똑같을 순 없어도 평균값으로 대체했을 때랑 너무 똑같기 때문에 이 경우는 문제를 찾아봐야 할 것 같다.
3.1.5 수치형 변수를 정규분포 형태로 만들기
우리가 데이터 전처리를 할 때 그래프가 왼쪽으로 너무 치우쳐져 있으면 제대로 된 학습이 어렵다.
-> 따라서 우리는 한쪽으로 몰려있는 데이터를 정규분포로 만들어주기도 한다.
그럼 인슐린 데이터의 분포부터 그려보도록 하자.
sns.distplot(df["Insulin"])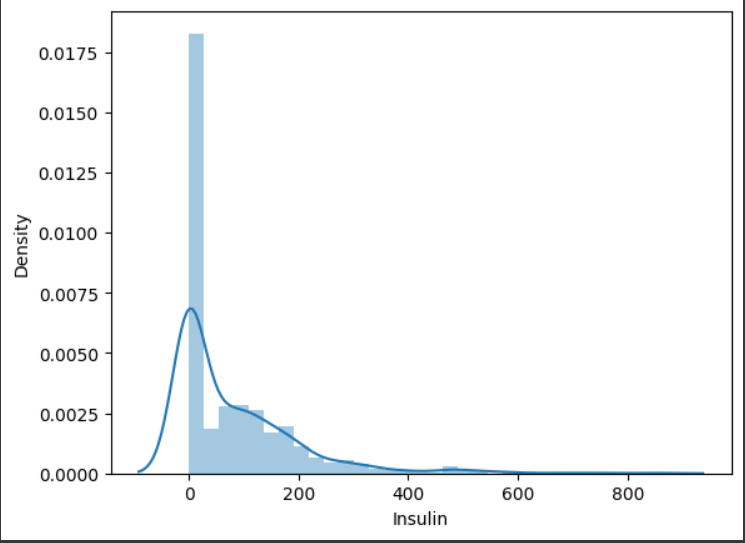
그래프를 보면 이렇게 한 쪽으로 치우쳐져 있고 0에 뾰족하게 몰려있는 것을 확인할 수 있다. 이는 0에 대해 전처리를 하기 전의 형태인데,
sns.distplot(df.loc[df["Insulin"] > 0, "Insulin"])따라서 0에 대해 전처리를 해보면
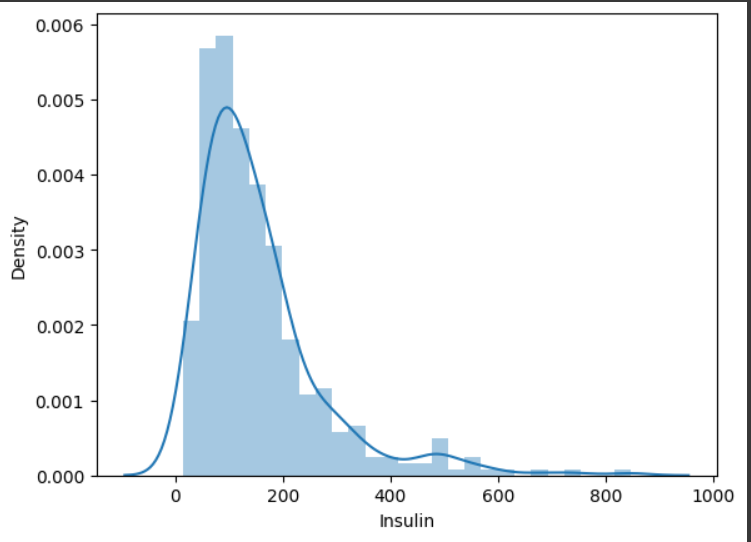
여전히 한 쪽으로 치우쳐져 있는 모습을 확인할 수 있다. 우리는 여기서 2가지 개념을 습득할 수 있다. 바로 "한쪽으로 치우쳐져 있는 정도"인 왜도와 "뾰족한 부분을 나타내는 것"을 첨도라고 한다. 지금 여기서는 결측치를 채우기 전이기 때문에 한쪽으로 뾰족한 모습이 나타나는 것이다.
------------------------------------------------------------------------
그럼 이렇게 치우친 값을 전처리 해볼 수는 없을까? 아니다 있다. 바로 log를 이용하는 것이다.
sns.distplot(np.log(df.loc[df["Insulin"] > 0, "Insulin"] + 1))위의 인슐린 그래프에 log를 씌어보면
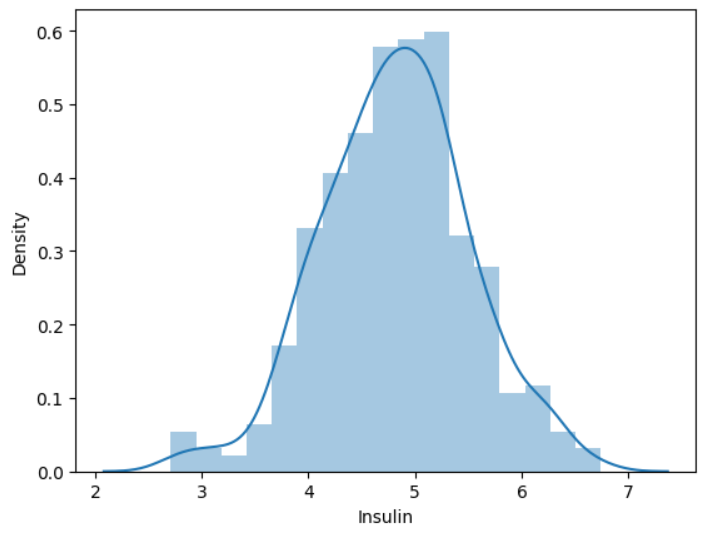
다음과 같이 정규분포의 형태로 나타나는 것을 확인할 수 있다. 위 코드에서 +1을 해준 이유는 0이하에서는 -값으로 수렴하기 때문이다.
그럼 이번에는 저 인슐린 값을 distplot으로 그려보는 작업을 수행해보자.
sns.distplot(df["Insulin_nan"])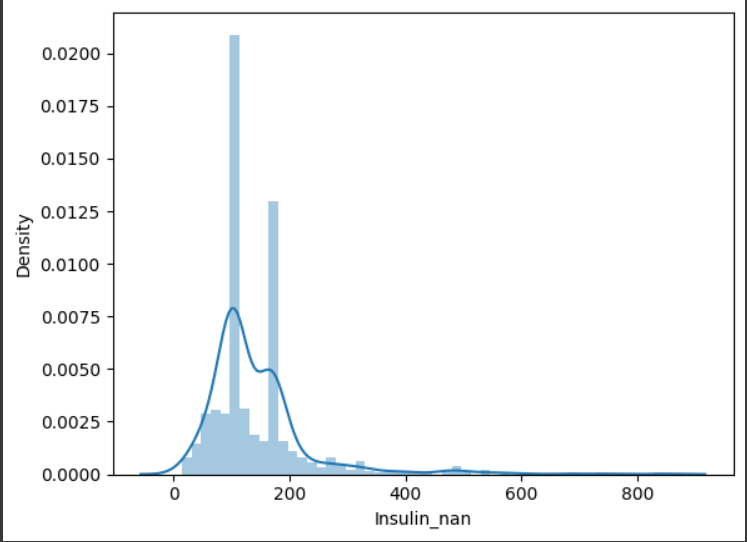
우리는 앞서 log를 통해 중앙값으로 그래프를 채워주었기 때문에 뾰족한 그래프(첨도)가 두 개가 나타나는 것을 확인할 수 있다. 그리고 또다른 특성은 그래프의 모양이 오른쪽으로 크게 꼬리지어 있다는 점이다.
그럼 이번에도 이 "Insulin_nan"의 그래프를 log를 씌어줘보자.
df["Insulin_log"] = np.log(df["Insulin_nan"] + 1)
sns.distplot(df["Insulin_log"])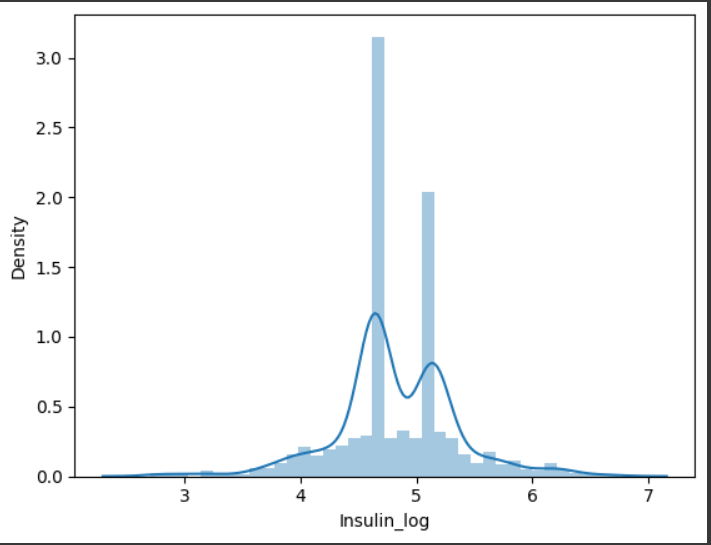
위에 코드를 작성할 때도 마찬가지로 로그에서 +1을 해주어서 그래프가 -값으로 수렴하는 것을 방지해주어야 한다.
그래프의 모양도 살펴보면 당뇨병 여부에 따라서 넣어준 값 때문에 역시나 긴 장대 2개가 생기는 것을 확인할 수 있다.
----------------------------------------------------------------------------------------------------
그러면 이제 "Insulin_log" 데이터를 넣어주면 학습에 어떤 영향이 있을지 확인해보러 가자.
# feature_names 라는 변수에 학습과 예측에 사용할 컬명을 가져옵니다.
feature_names = train.columns.tolist()
feature_names.remove("Pregnancies")
feature_names.remove("Outcome")
feature_names.remove("Age_low")
feature_names.remove("Age_middle")
feature_names.remove("Age_high")
feature_names.remove("Insulin")
feature_names.remove("Insulin_nan")
feature_names
여기서는 제거해야할 값으로 "Insulin_nan" 없애주었다. 그 이유는 "Insulin_log"를 이용해야 하기 때문에 겹치면 안되기 때문이다.
따라서 여기서 확인해야될 점은 학습, 예측 데이터셋을 만드는 부분인데,
# 학습 세트 만들기 예) 시험의 기출문제
X_train = train[feature_names]
print(X_train.shape)
X_train.head()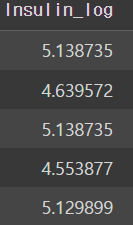
인슐린 데이터에 로그를 취해주어서 값의 차이들이 많이 줄어든 것을 확인할 수 있다.
그리고 트리 시각화 부분도 확인해보면
from sklearn.tree import plot_tree
plt.figure(figsize=(20,20))
tree = plot_tree(model,
feature_names=feature_names,
filled=True,
fontsize=10)
여전히 인슐린 부분이 가장 높은 자리를 차지하며 신뢰성이 높다는 것을 확인할 수 있다.
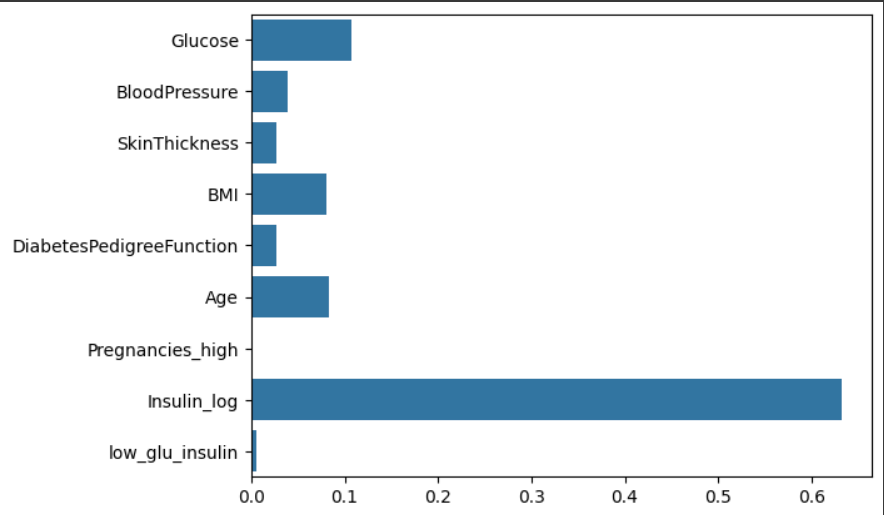
그리고 추가로 해당 실습에서는 "정확도(Accuracy) 측정하기" 부분에서 정확도가 변하지 않았지만, log를 씌어줌으로써 정확도가 올라가는 현상을 보일 수도 있다고 한다.
3.1.6 상관 분석을 통해 파생변수 만들기
이번에는 EDA를 할 때 상관계수 구했던 자료들을 어떻게 피처 엔지니어링에 사용하는지를 보도록 하자.
그럼 만들어줬던 상관계수 HEATMAP에서 상관계수가 높은 수치를 확인해보자.
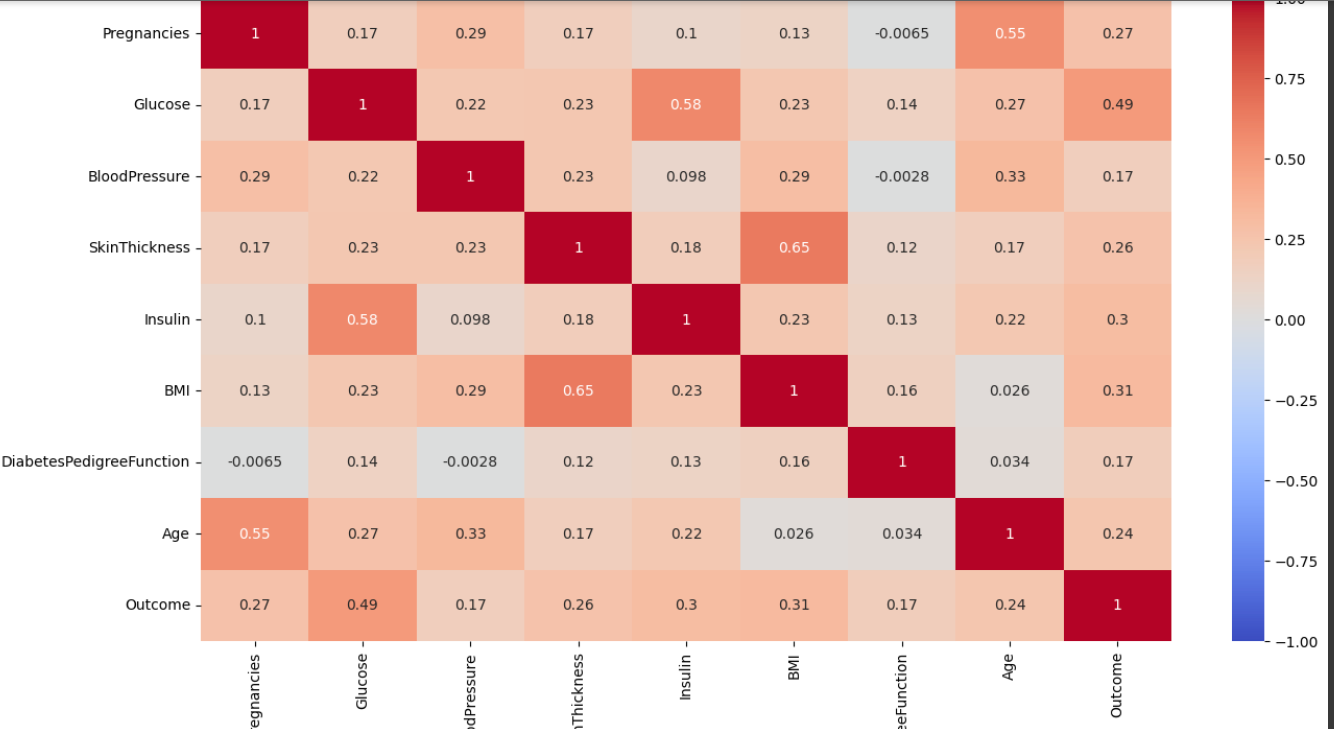
여기서 Insulin과 Glucose의 상관계수가 0.58로 높은 것을 확인할 수 있고, BMI와 Sthickness가 0.65로 높은 것을 확인할 수 있다.
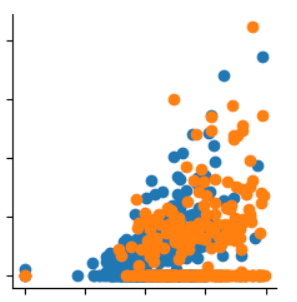
Insulin과Glucose
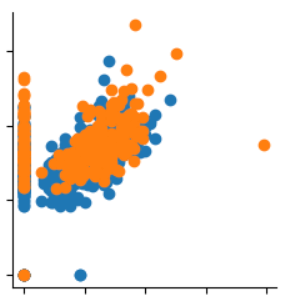
BMI와Skinthickness
먼저 BMI와 Skinthickness의 pairplot을 보면 상관관계는 높지만 경계가 뚜렷하게 드러나지 않는 것을 확인할 수 있고,
Insulin과 Glucose를 보면 겹쳐져서 보이기는 하나, 아랫부분에 인슐린과 글루코스 분포는 발병율이 굉장히 낮은 것처럼 보여진다.
그러면 이 그래프를 outcome값을 적절히 보기위해 lmplot으로 그려보고자 한다.
sns.lmplot(data=df_matrix, x="Insulin", y="Glucose", hue="Outcome")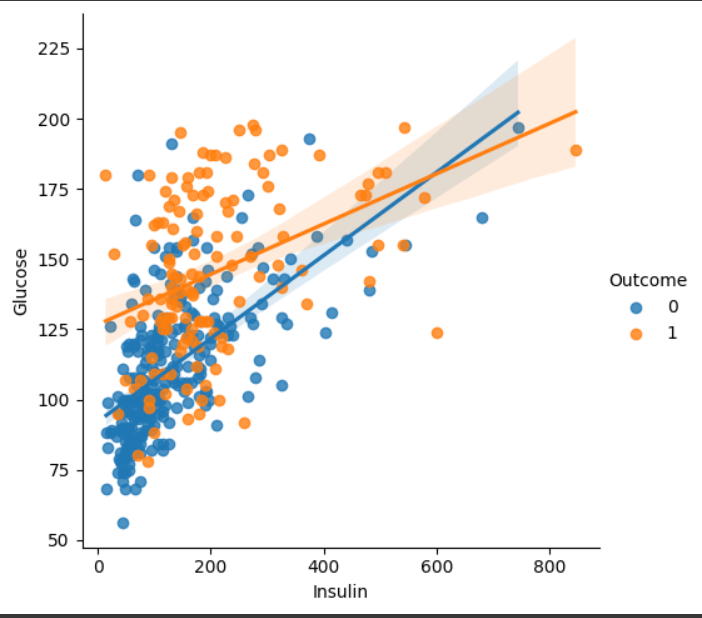
이 그래프를 살펴보면 Glucose의 값과 Insulin의 값이 모두 100이하인 사람들은 대부분 발병하지 않는 것을 확인할 수 있다. 이런 구간은 우리가 따로 변수를 만들어줄 수 있다.
sns.lmplot(data=df, x="Insulin_nan", y="Glucose", hue="Outcome")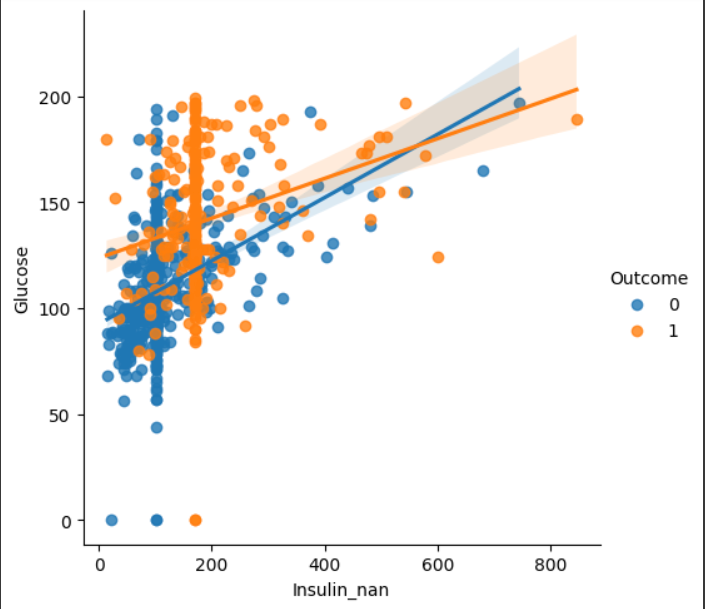
glucose 값을 100이하로 설정하고 시각화해보면 파란일자선, 주황일자선이 하나씩 나오는데, 이것은 우리가 직접 채워준 값이다. glucose는 100이하에서, Insulin 값도 중앙값(102.5)로 채워줬다.
------------------------------------------------------
그럼 이 기준값을 수치적으로 활용하여 결론을 도출해보자.
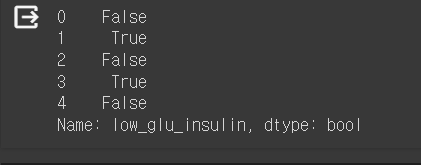
df["low_glu_insulin"] = (df["Glucose"] < 100) & (df["Insulin_nan"] <= 102.5)
df["low_glu_insulin"].head()Glucose와 Insulin_nan의 기준을 설정해준 변수를 생성하고 미리보기를 한다.
pd.crosstab(df["Outcome"], df["low_glu_insulin"])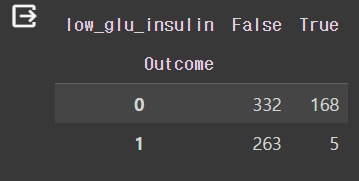
그런 다음 실제 Outcome값과 low_glu_insulin 값이 얼마나 연관성이 있는지 살펴보니 Outcome 값이 1일 때 low_glu_insulin에 포함되는 값이 5개밖에 없었던 것으로 보아 글루코스의 값이 100보다 작고, 인슐린 값이 102.5보다 작을 때 당뇨병 발병이 정말 작아진다고 추측할 수 있다.
-------------------------------------------------------------------------------------------------------------------------
그러면 우리가 파생변수를 만들어준 이후에 정확도는 어떻게 변했을까?
# 실제값 - 예측을 빼주 같은 값은 0으로 나오게 됩니다.
# 여기에서 절대값을 씌운 값이 1인 값이 다르게 예측한 값이 됩니다.
diff_count = abs(y_test - y_predict).sum()
diff_count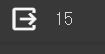
-----
# 예측의 정확도를 구합니다. 100점 만점 중에 몇 점을 맞았는지 구한다고 보면 됩니다.
(len(y_test) - diff_count) / len(y_test) * 100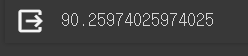
--------------
# 위에서 처럼 직접 구할 수도 있지만 미리 구현된 알고리즘을 가져와 사용합니다.
from sklearn.metrics import accuracy_score
accuracy_score(y_test, y_predict)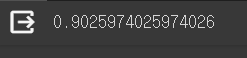
----------
# model 의 score 로 점수를 계산합니다.
model.score(X_test, y_test) * 100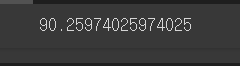
놀랍게도 정확도가 상승한 것으로 보아, 파생변수를 만들어 준 것이 효과적이었다고 볼 수 있다.
----------------------------------------------------------------------------------------------------------------------------------------------------------
3.1.7 이상치(Outlier) 다루기
이번에는 피쳐 엔지니어링 기법 중 이상치 다루기에 대해 알아보겠다.
정확도를 높이기 위해 우리는 '이상치'를 제거해주는 것이 좋다.
이때 이상치를 확인하기 위해서 보통 '상자 수염 그림'(boxplot)을 이용한다.
우리는 이를 통해 5가지 요약 수치(최솟값, 제1사분위(Q1), 제 2사분위 (Q2) , 제 3사분위 (Q3) , 제 4사분위 (Q4) , 최댓값)에 대해 알 수 있다.
여러 데이터 중 인슐린 수치에 대해서 상자그림을 그려보겠다.
이때 결측치를 처리 안한 인슐린 값은 0에 붙어서 그림이 그려지므로 결측치 처리한 값을 보겠다.
plt.figure(figsize=(15, 2))
sns.boxplot(df["Insulin_nan"])
여기서 600개 이상의 값이 3개 있는 것을 볼 수 있다. 이는 다른 값과 차이가 많이 난다.
describe()로 데이터를 살펴보자.
df["Insulin_nan"].describe()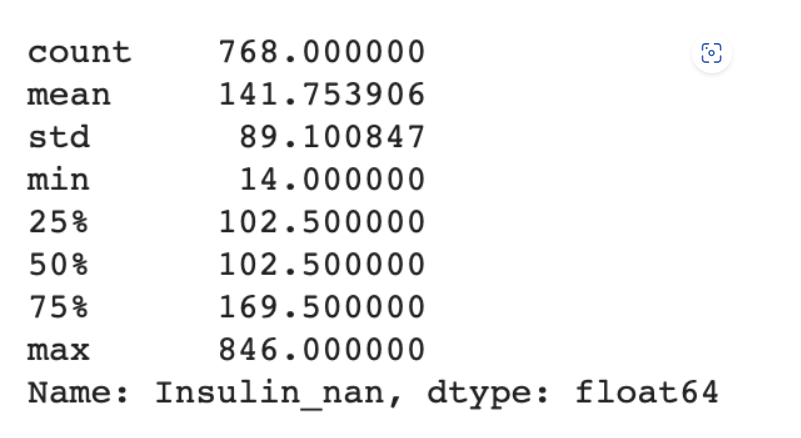
25%와 50%가 같은 이유는 null 값을 중앙값으로 채워줬기 때문이고, max 값이 크기 때문에 평균값이 높다.
25%가 상자의 시작 값, 75%가 상자의 마지막 값, 50%은 중간 선을 의미한다.(현재 그림에서는 25%와 50%이 같아 나타나지 않았다.)
max값과 75%의 값이 차이가 많이 난다.
이때 상자 수염 그림에서는 이상치를 Q3보다 1.5IQR 이상 초과하는 값과 Q1보다 1.5IQR이상 미달하는 값으로 정의한다.
여기서 IQR이란 (Q3-Q1)이다.
위의 식을 통해 계산해 이를 구해보자.
IQR3 = df["Insulin_nan"].quantile(0.75)
IQR1 = df["Insulin_nan"].quantile(0.25)
IQR = IQR3 - IQR1
OUT = IQR3 + (IQR * 1.5)이때 이상치 값은 270이 나온다. 즉 270 이상부터 이상치로 보는 것이다.
270이상인 값을 알아보자.
df[df["Insulin_nan"] > OUT].shape이때 답은 (51,16)으로 51개가 나온다. 제거하기엔 많은 양이 나오니 먼저 600이상인 값들만 제거해보자.
train = train[train["Insulin_nan"] < 600]test에서가 아닌 train값에서만 제거를 해준다.
이 경우 정확도에 큰 차이가 없었다.
이때 계산한 값(270)이 이상한 이유는 보통 boxplot은 정규분포에 사용되기 때문이다.
따라서 정규분포와 비슷한 Insulin_log를 기준으로 이상치 값을 알아보자.
#정규분포 이상치
import numpy as np
# Insulin_nan 열의 값에 로그를 취합니다. 이 때, np.log1p 함수를 사용하여 0인 경우를 대비합니다.
df['Insulin_log'] = np.log1p(df['Insulin_nan'])
df["Insulin_log"].describe()결측치를 제거한 Insulin값에 log를 취하고 그 값들을 살펴보면 다음과 같다.
count 394.000000
mean 4.818456
std 0.691261
min 2.708050
25% 4.347031
50% 4.836282
75% 5.252273
max 6.741701
Name: Insulin_log, dtype: float64최소가 2.7 최대가 6.7 등 여러 정보를 확인할 수 있다.
이를 boxplot으로 나타내면 다음과 같다.
plt.figure(figsize=(15,2))
sns.boxplot(df["Insulin_log"])
이상치를 계산해보자.
IQR3=df["Insulin_log"].quantile(0.75)
IQR1=df["Insulin_log"].quantile(0.25)
IQR = IQR3-IQR1
OUT1 = IQR3 + (IQR *1.5)
OUT2 = IQR1 - (IQR *1.5)
print(OUT1)
print(OUT2)값은 6.610136660522583, 2.989168040586707으로 그래프와 정보와 비교하였을 때 우리가 찾는 이상치 임을 알 수 있다. 따라서 Insulin_nan에서 값이 유의미하지 못했던 이유는 정규분포가 아닌 곳에 식을 적용했기 때문이다.
이렇게 boxplot을 이용하여 이상치를 찾아보았다. 이렇게 찾은 이상치를 제거하는 것은 정확도를 올리는 방법 중 하나이다.
3.1.8 -> 피쳐 스케일링
피쳐 스케일링 - 데이터 크기 맞추기
우리가 모델을 만들때 때로는 데이터간의 범위가 너무 차이가 나서 모델의 성능에 영향을 줄 때가 있다.예를 들어 몸무게와 키의 경우, 데이터의 범위가 차이가 나는데 이를 하나의 모델에 넣게 되면 데이터의 범위가 훨씬 넓어져 키가 몸무게에 비해 모델에 과다하게 영향을 줄 수 있다 .
일반적으로 스케일링을 위한 전략이 두 가지가 있다. 하나는 '최솟값-최댓값 정규화(min-max normalization), 다른 하나는 'z-스코어 정규화(z-score normalization)이다.
1. '최솟값-최댓값' 정규화(min-max normalization)
최솟값과 최댓값을 기준으로 0 에서 1, 또는 0 에서 지정값까지 값의 크기를 변화시키는 기법이다. 이때 이상치가 있을 경우 값의 분포가 왜곡될 수 있다.
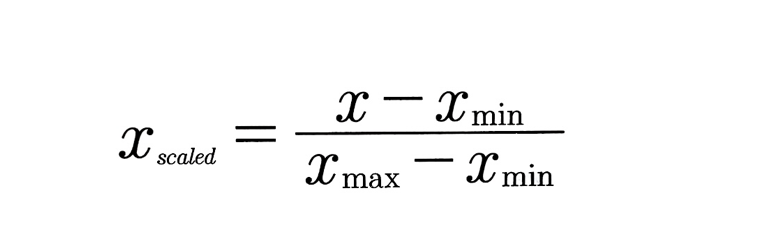
(df['A']-df['A'].min()) / (df['A'].max()-df['A'].min())
2. z-스코어 정규화(z-score normalization)
기존 값을 표준 정규분포 값으로 변환하여 처리하는 기법이다.
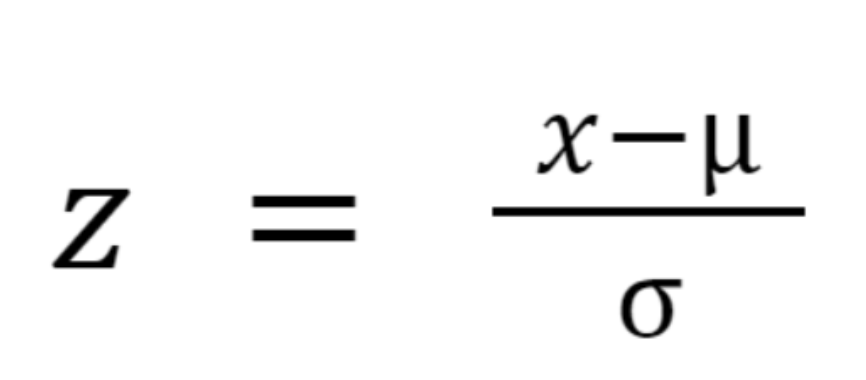
(df['B'] - df['B'].mean()) / df['B'].std())
과연 스케일링이 반드시 모델 성능에 유의미한 영향을 끼칠까? -> 그렇지 않다. 스케일링을 하게 되면 원래 분포가 가지는 의미를 잃을 수 있다. 따라서 각각의 변수에 다른 다양한 스케일링을 해보면서, 모델의 성능이 올라가는지 그렇지 않은지를 관찰해야 한다.
4.1.1 사이킷런을 통해 학습과 예측에 사용할 데이터셋 나누기
- 사이킷런에서 지원되는 train_test_split를 통해 학습과 예측에 사용될 데이터 셋을 나눌 수 있다.
from sklearn.model_selection import train_test_split
train_test_split(arrays, test_size, train_size, random_state, shuffle, stratify)
파라미터 설명
arrays: 분할시킬 데이터를 입력(리스트,배열,데이터 프레임)
test_size: 테스트 데이터셋의 비율(default = 0.25)
train_size: 학습 데이터셋의 비율( default = test_size의 나머지)
random_state: 데이터 분할시 셔플이 이루어지는데 이를 위한 시드값(강의에서는 42로 고정함)
shuffle: 셔플을 할지 말지 여부를 결정
stratify: 지정한 Data의 비율을 유지한다. 예를 들어, Label Set인 Y가 25%의 0과 75%의 1로 이루어진 Binary Set일 때, stratify=Y로 설정하면 나누어진 데이터셋들도 0과 1을 각각 25%, 75%로 유지한 채 분할된다.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42)실제 코드
4.1.2 ~ 4.1.3 max_depth값을 바꿔가며 decision tree로 학습 ,예측
정보 분할 계수
지니 계수(Gini index) : 불순도를 측정하는 척도로서 데이터의 통계적 분산정도를 정량화해서 표현한 값이다.
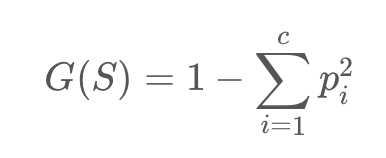
지니 계수의 식
S: 이미 발생한 사건들 c: 사건의 개수 p: 전체 사건 중에서 특정 사건의 수 --> 지니 계수가 높을 수록 데이터가 분산되어 있음을 의미
엔트로피(Entropy): 정보 이론에서, 정보의 불확실함의 정도를 나타내는 양
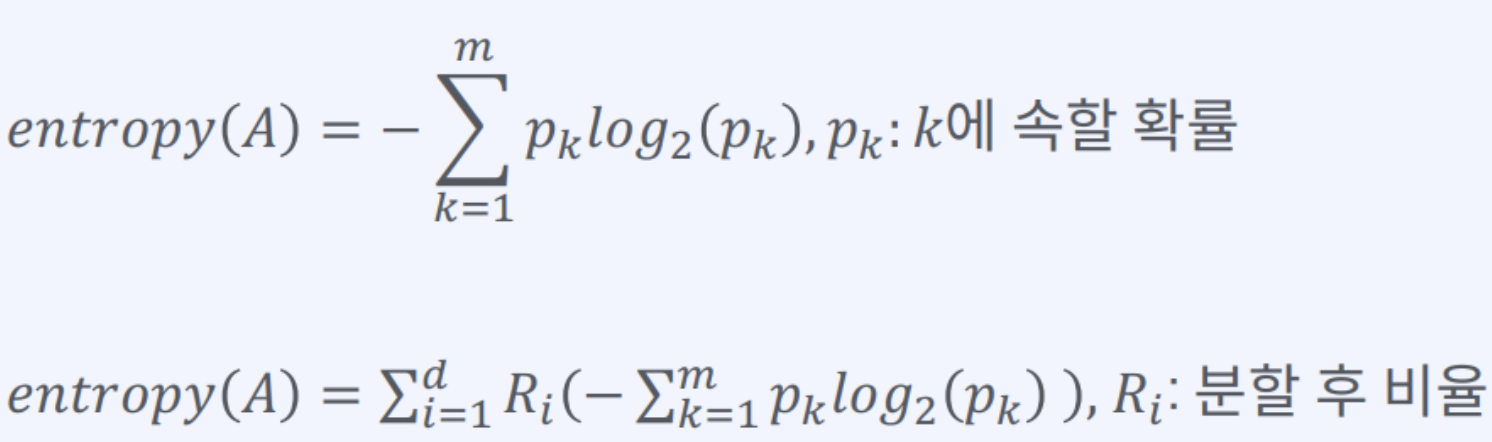
엔트로피 계수의 식
from sklearn.metrics import accuracy_score
for max_depth in range(3, 12):
model = DecisionTreeClassifier(max_depth=max_depth, random_state=42)
y_predict = model.fit(X_train, y_train).predict(X_test)
score = accuracy_score(y_test, y_predict) * 100
print(max_depth, score)
해당 코드는 max_depth의 깊이를 바꿔가며 모델의 정확도를 비교하는 코드이다, 주의해야할 점은 max_depth의 깊이가 길어질수록 과대적합이 일어날 수 있고, 깊이가 너무 얕으면 언더피팅이 일어날 수 있다.
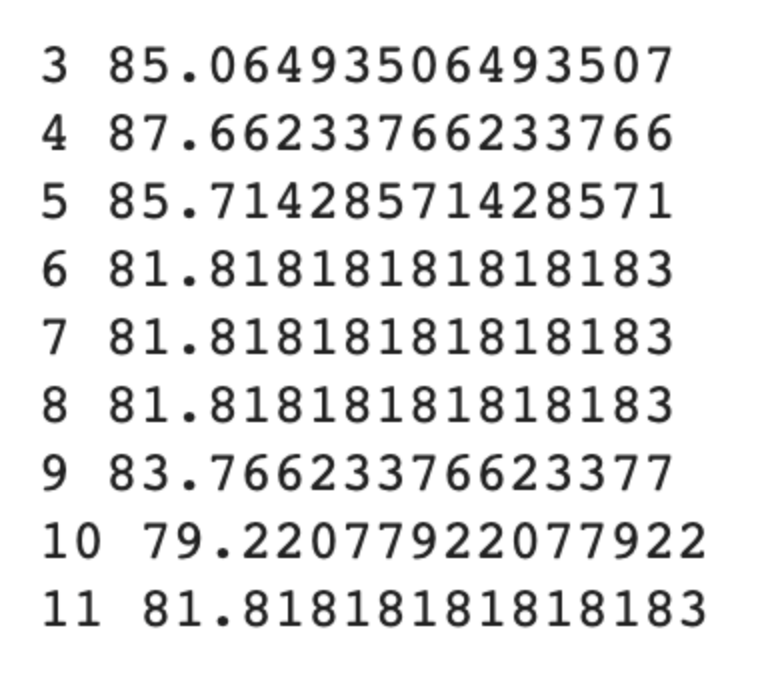
max_depth를 바꿔가며 도출한 정확도
'Study > CODE 2기 [프로젝트로 배우는 데이터사이언스]' 카테고리의 다른 글
| [삼위일체(3조)] 프로젝트로 배우는 데이터 사이언스_3주차 (0) | 2024.03.25 |
|---|---|
| [All in One(2조)] 프로젝트로 배우는 데이터사이언스_3주차 (0) | 2024.03.25 |
| [Trillion(1조)] 프로젝트로 배우는 데이터사이언스_2주차 (0) | 2024.03.18 |
| [All in One(2조)] 프로젝트로 배우는 데이터사이언스_2주차 (1) | 2024.03.18 |
| [삼위일체(3조)] 프로젝트로 배우는 데이터 사이언스_2주차 (0) | 2024.03.18 |



