작성자 : 오동진
작성일 : 2023-03-23
진도 : Import & Data Check
-데이터 확인
SalePrice (부동산 판매가격으로 예측하려는 대상 변수)에 영향을 미치는 약 80개의 데이터들 확인하기
EX) LotArea : 부지 크기(제곱피트), Street : 도로 접근 유형, OverallQual : 전반적인 재료 및 마감 품질, TotalBsmtSF : 지하 면적의 총 평방 피트, GrLivArea : 지상(지상) 거실 면적 평방피트, GarageCars : 차량 수용 가능 차고의 크기, FullBath : 지상 위의 전체 욕실, YearBuilt : 원래 건설 날짜, YearRemodAdd : 리모델링 날짜 등
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os
from collections import Counter
plt.style.use('seaborn')
sns.set(font_scale=1.5)
import missingno as msno
import warnings
warnings.filterwarnings("ignore")
%matplotlib inlinetrain_df = pd.read_csv("train.csv")
test_df = pd.read_csv("test.csv")
print(train_df.shape, test_df.shape)
train_df.head(5)
google colab을 사용하여 진행했고 파일을 직접 업로드 했기 때문에 경로를 지정할 필요 없이 데이터를 불러옵니다.
데이터 프레임의 형태를 확인해줍니다. train.csv는 학습시킬 데이터, test.csv는 테스트할 데이터입니다.
데이터들을 numerical_feats과 categofical_feats으로 나눠 데이터프레임을 구분해줍니다.

def detect_outliers(df, n, features):
outlier_indices = []
for col in features:
Q1 = np.percentile(df[col], 25)
Q3 = np.percentile(df[col], 75)
IQR = Q3 - Q1
outlier_step = 1.5 * IQR
outlier_list_col = df[(df[col] < Q1 - outlier_step) | (df[col] > Q3 + outlier_step)].index
outlier_indices.extend(outlier_list_col)
outlier_indices = Counter(outlier_indices)
multiple_outliers = list(k for k, v in outlier_indices.items() if v > n)
return multiple_outliers
Outliers_to_drop = detect_outliers(df_train, 2, ['Id', 'MSSubClass', 'LotFrontage', 'LotArea', 'OverallQual',
'OverallCond', 'YearBuilt', 'YearRemodAdd', 'MasVnrArea', 'BsmtFinSF1',
'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF', '2ndFlrSF',
'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd',
'Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea', 'WoodDeckSF',
'OpenPorchSF', 'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea',
'MiscVal', 'MoSold', 'YrSold'])
df_train = df_train.drop(Outlier_to_drop, axis = 0).reset_index(drop=True)
df_train.shape정의한 함수를 이용하여 outliers를 제거하고 형태를 확인해보면 (1338, 81)로 행의 수가 줄어든 것을 확인할 수 있습니다.
for col in df_train.columns:
msperc = 'column: {:>10}\t Percent of NaN value: {:.2f}%'.format(col, 100 * (df_train[col].isnull().sum() / df_train[col].shape[0]))
print(msperc)train data의 각 column의 결측치가 몇%인지 확인합니다.
for col in df_train.columns:
msperc = 'column: {:>10}\t Percent of NaN value: {:.2f}%'.format(col, 100 * (df_train[col].isnull().sum() / df_train[col].shape[0]))
print(msperc)
test 데이터에서도 같은 방식으로 결측치를 확인합니다.
missing = df_train.isnull().sum()
missing = missing[missing > 0]
missing.sort_values(inplace=True)
missing.plot.bar(figsize = (12,6))
# 직관적으로 확인하기 위해 barplot을 그려봅니다.
for col in numerical_feats:
print('{:15}'.format(col),
'Skewness: {:05.2f}'.format(df_train[col].skew()) ,
' ' ,
'Kurtosis: {:06.2f}'.format(df_train[col].kurt())
)수치형 변수의 Skewness(비대칭도), Kurtosis(첨도)를 확인합니다.
이는 분포가 얼마나 비대칭을 띄는가 알려주는 척도입니다.
비대칭도는 분포가 정규분포에서 얼마나 벗어나 있는지를 나타내며, 0에 가까울수록 정규분포에 가까워집니다/
첨도는 분포의 꼬리 부분이 얼마나 두터운지를 나타내며, 0에 가까울수록 정규분포에 가까워집니다.
쉽게 말하면 해당 값들이 0에 가까울수록 정규분포에 가깝다고 할 수 있습니다.

작성자 : 박지혜
작성일 : 2023-03-24
진도 : EDA
다음은 EDA(exploratory data analysis탐색적 데이터 분석) 입니다.
4가지의 그래프를 그립니다.
첫번째는 Correlation Heat Map(상관분석 히트맵)입니다.
주택가격과 관련된 모든 변수들을 제시하여 그 중 상관관계가 제일 큰 부분을 찾습니다.
corr_data = df_train[['Id', 'MSSubClass', 'LotFrontage', 'LotArea', 'OverallQual',
'OverallCond', 'YearBuilt', 'YearRemodAdd', 'MasVnrArea', 'BsmtFinSF1',
'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', '1stFlrSF', '2ndFlrSF',
'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd',
'Fireplaces', 'GarageYrBlt', 'GarageCars', 'GarageArea', 'WoodDeckSF',
'OpenPorchSF', 'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea',
'MiscVal', 'MoSold', 'YrSold', 'SalePrice']]
colormap = plt.cm.PuBu
sns.set(font_scale=1.0)
f , ax = plt.subplots(figsize = (14,12))
plt.title('Correlation of Numeric Features with Sale Price',y=1,size=18)
sns.heatmap(corr_data.corr(),square = True, linewidths = 0.1,
cmap = colormap, linecolor = "white", vmax=0.8)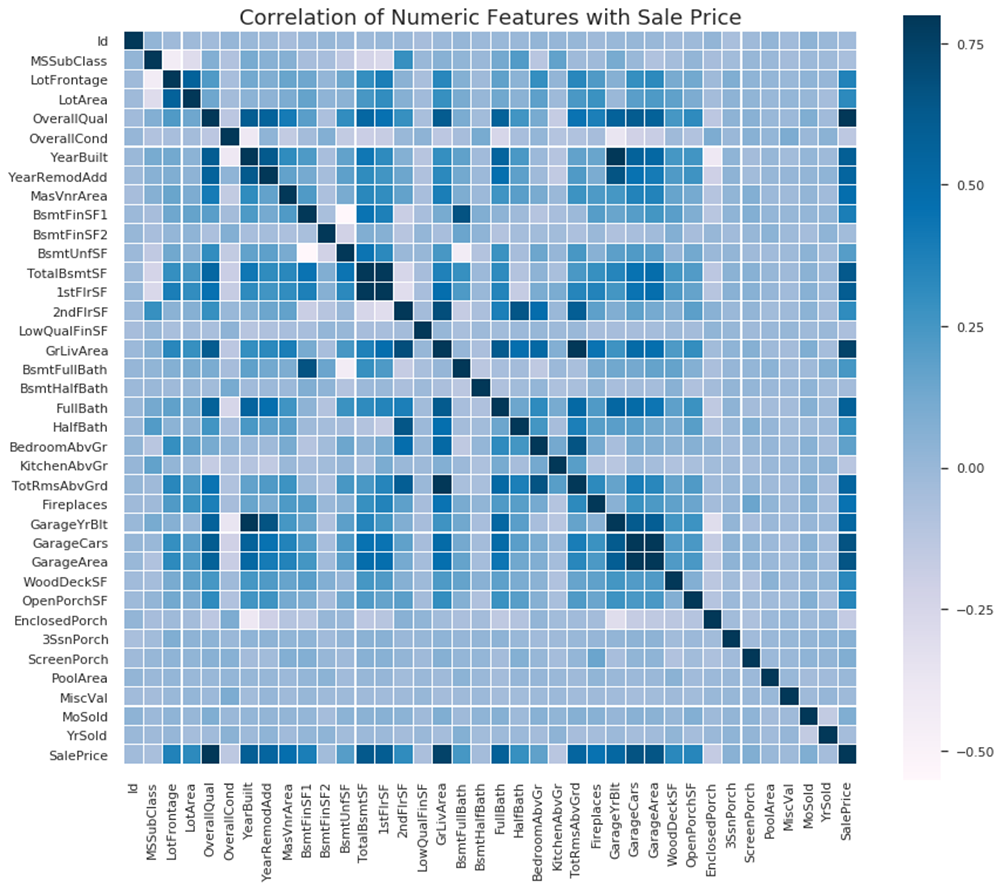
제일 우측에 있는 SalePrice가 중점이고, 파란색의 변화를 살펴보면 OverallQual(전반적인 재료 및 마감 품질), GrLivArea(지상 거실 면적 평방피트)이 2개 변수가 주택가격과의 상관성이 제일 크다고 봅니다. 주택가격에 상대적으로 큰 영향(>0)을 미치는 모든 변수들을 다시 살펴봅니다. 이를 위해 Zoomed Heat Map(확대된 히트맵)을 그립니다.
k= 11
cols = corr_data.corr().nlargest(k,'SalePrice')['SalePrice'].index
print(cols)
cm = np.corrcoef(df_train[cols].values.T)
f , ax = plt.subplots(figsize = (12,10))
sns.heatmap(cm, vmax=.8, linewidths=0.1,square=True,annot=True,cmap=colormap,
linecolor="white",xticklabels = cols.values ,annot_kws = {'size':14},yticklabels = cols.values)

가장 눈에 띄는 GarageCars (차량 수용 가능 차고의 크기)
와 GarageArea,(평방 피트 단위의 차고 크기) TotalBsmtSF(지하 면적의 총 평방 피트) 와 1stFlrSF(1층 평방 피트)
는 서로 밀접하게 연관되어 있음을 알 수 있습니다. Target feature와 가장 밀접한 연관이 있는 feature는 'OverallQual', 'GrLivArea'및 'TotalBsmtSF'로 보입니다.
먼저 말했던 GarageCars와 GarageArea, TotalBsmtSF와 1stFlrSF, TotRmsAbvGrd(지상 위의 총 객실 수(욕실 제외))
와 GrLivArea는 모두 매우 유사한 정보를 포함하고 있으며 다중공선성이 나타난다고 할 수 있습니다.
SalePrice와 더 연관되어있는 변수인 GarageCars와 TotalBsmtSF, GrLivArea를 남기고 나머지는 이후에 버리도록 합니다.
SalePrice와의 연관을 더 알아보기 위해 PairPlot을 그려보도록 합니다.
sns.set()
columns = ['SalePrice','OverallQual','TotalBsmtSF','GrLivArea','GarageCars','FullBath','YearBuilt','YearRemodAdd']
sns.pairplot(df_train[columns],size = 2 ,kind ='scatter',diag_kind='kde')
plt.show()
Pair Plot은 한눈에 볼 수 있지만, 그래프가 좀 복잡해서 Scatter Plot를 그려 각 변수가 SalePrice과의 연관을 더 잘 살펴볼 수 있습니다.
fig, ((ax1, ax2), (ax3, ax4),(ax5,ax6)) = plt.subplots(nrows=3, ncols=2, figsize=(16,13))
OverallQual_scatter_plot = pd.concat([df_train['SalePrice'],df_train['OverallQual']],axis = 1)
sns.regplot(x='OverallQual',y = 'SalePrice',data = OverallQual_scatter_plot,scatter= True, fit_reg=True, ax=ax1)
TotalBsmtSF_scatter_plot = pd.concat([df_train['SalePrice'],df_train['TotalBsmtSF']],axis = 1)
sns.regplot(x='TotalBsmtSF',y = 'SalePrice',data = TotalBsmtSF_scatter_plot,scatter= True, fit_reg=True, ax=ax2)
GrLivArea_scatter_plot = pd.concat([df_train['SalePrice'],df_train['GrLivArea']],axis = 1)
sns.regplot(x='GrLivArea',y = 'SalePrice',data = GrLivArea_scatter_plot,scatter= True, fit_reg=True, ax=ax3)
GarageCars_scatter_plot = pd.concat([df_train['SalePrice'],df_train['GarageCars']],axis = 1)
sns.regplot(x='GarageCars',y = 'SalePrice',data = GarageCars_scatter_plot,scatter= True, fit_reg=True, ax=ax4)
FullBath_scatter_plot = pd.concat([df_train['SalePrice'],df_train['FullBath']],axis = 1)
sns.regplot(x='FullBath',y = 'SalePrice',data = FullBath_scatter_plot,scatter= True, fit_reg=True, ax=ax5)
YearBuilt_scatter_plot = pd.concat([df_train['SalePrice'],df_train['YearBuilt']],axis = 1)
sns.regplot(x='YearBuilt',y = 'SalePrice',data = YearBuilt_scatter_plot,scatter= True, fit_reg=True, ax=ax6)
YearRemodAdd_scatter_plot = pd.concat([df_train['SalePrice'],df_train['YearRemodAdd']],axis = 1)
YearRemodAdd_scatter_plot.plot.scatter('YearRemodAdd','SalePrice')
Target Feature "SalePrice"와 가장 밀접한 연관이 있다고 판단됐던 변수들의 Scatter Plot을 그립니다.
변수와 SalePrice 간의 상관관계 파악: Scatter Plot을 통해 변수와 SalePrice 간의 상관관계를 파악할 수 있습니다. 만약 Scatter Plot이 일직선에 가깝게 분포한다면, 변수와 SalePrice 간에 강한 선형관계가 있을 가능성이 높습니다. 반면, Scatter Plot이 뭉쳐져 있거나 양 끝단에 이상치가 존재한다면, 변수와 SalePrice 간의 선형관계가 약하거나 비선형적인 관계일 가능성이 있습니다.
OverallQual, GarageCars, Fullbath와 같은 변수들은 실제로는 범주형 데이터의 특징을 보인다고 할 수 있습니다. (등급, 개수 등을 의미하기 때문)
for catg in list(categorical_feats) :
print(df_train[catg].value_counts())
print('#'*50)
li_cat_feats = list(categorical_feats)
nr_rows = 15
nr_cols = 3
fig, axs = plt.subplots(nr_rows, nr_cols, figsize=(nr_cols*4,nr_rows*3))
for r in range(0,nr_rows):
for c in range(0,nr_cols):
i = r*nr_cols+c
if i < len(li_cat_feats):
sns.boxplot(x=li_cat_feats[i], y=df_train["SalePrice"], data=df_train, ax = axs[r][c])
plt.tight_layout()
plt.show()

BoxPlot을 그려 Categorical Feature와 SalePrice의 관계를 확인합니다.
일부 범주는 다른 범주보다 SalePrice와 관련하여 더 다양하게 보입니다.
Neighborhood 변수는 주택 가격 편차가 매우 크므로 영향이 크다고 생각됩니다.
SaleType 또한 마찬가지입니다.
또한 수영장이 있으면 가격이 크게 증가하는 것 같습니다.
정리하면 SalePrice에 영향을 많이 끼치는 변수는 'MSZoning', 'Neighborhood', 'Condition2', 'MasVnrType', 'ExterQual', 'BsmtQual', 'CentralAir', 'Electrical', 'KitchenQual', 'SaleType' 등이 있습니다.
num_strong_corr = ['SalePrice','OverallQual','TotalBsmtSF','GrLivArea','GarageCars',
'FullBath','YearBuilt','YearRemodAdd']
num_weak_corr = ['MSSubClass', 'LotFrontage', 'LotArea', 'OverallCond', 'MasVnrArea', 'BsmtFinSF1',
'BsmtFinSF2', 'BsmtUnfSF', '1stFlrSF', '2ndFlrSF','LowQualFinSF', 'BsmtFullBath',
'BsmtHalfBath', 'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'TotRmsAbvGrd',
'Fireplaces', 'GarageYrBlt', 'GarageArea', 'WoodDeckSF','OpenPorchSF',
'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'MiscVal', 'MoSold', 'YrSold']
catg_strong_corr = ['MSZoning', 'Neighborhood', 'Condition2', 'MasVnrType', 'ExterQual',
'BsmtQual','CentralAir', 'Electrical', 'KitchenQual', 'SaleType']
catg_weak_corr = ['Street', 'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
'LandSlope', 'Condition1', 'BldgType', 'HouseStyle', 'RoofStyle',
'RoofMatl', 'Exterior1st', 'Exterior2nd', 'ExterCond', 'Foundation',
'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinType2', 'Heating',
'HeatingQC', 'Functional', 'FireplaceQu', 'GarageType', 'GarageFinish',
'GarageQual', 'GarageCond', 'PavedDrive', 'PoolQC', 'Fence', 'MiscFeature',
'SaleCondition' ]
SalePrice에 큰 영향을 미치는 변수와 상대적으로 크지 않은 영향을 미치는 변수를 분리합니다. 지하실과 생활공간의 면적, 이웃, 욕조, 퀄리티, 차고, 준공날짜, 리모델링 날짜, 이 변수들이 주택가격에 영향이 제일 크다고 봅니다.
작성자 : 박시현
작성일 : 2023-03-25
진도 : Feature Engineering (input 22 ~ input 28)
- Log 변환
f, ax = plt.subplots(1, 1, figsize = (10,6))
g = sns.distplot(df_train["SalePrice"], color = "b", label="Skewness: {:2f}".format(df_train["SalePrice"].skew()), ax=ax)
g = g.legend(loc = "best") #최적의 위치에 범례 추가
print("Skewness: %f" % df_train["SalePrice"].skew())
print("Kurtosis: %f" % df_train["SalePrice"].kurt())
sns.distplot() 는 주어진 데이터의 분포를 시각화하는 함수로 히스토그램과 커널 밀도 그래프를 함께 출력하며, 추가적으로 막대 그래프와 정규 분포 곡선을 겹쳐서 출력할 수도 있습니다. 이 코드를 통해서 데이터의 비대칭성과 첨도를 확인합니다. 아래는 위의 코드의 결과값입니다.

그래프를 확인하면 그래프가 positive skewed한 것을 확인할 수 있습니다. 이 데이터들을 분석에 용이하게 하기 위해 정규분포 모양으로 바꿔줍니다. 이를 위해서는 positive skewed한 부분을 줄여주는 로그 변환을 수행합니다.
df_train["SalePrice_Log"] = df_train["SalePrice"].map(lambda i:np.log(i) if i>0 else 0)
f, ax = plt.subplots(1, 1, figsize = (10,6))
g = sns.distplot(df_train["SalePrice_Log"], color = "b", label="Skewness: {:2f}".format(df_train["SalePrice_Log"].skew()), ax=ax)
g = g.legend(loc = "best")
print("Skewness: %f" % df_train['SalePrice_Log'].skew())
print("Kurtosis: %f" % df_train['SalePrice_Log'].kurt())
df_train.drop('SalePrice', axis= 1, inplace=True) #df_train에서 'SalePrice' 열을 제거
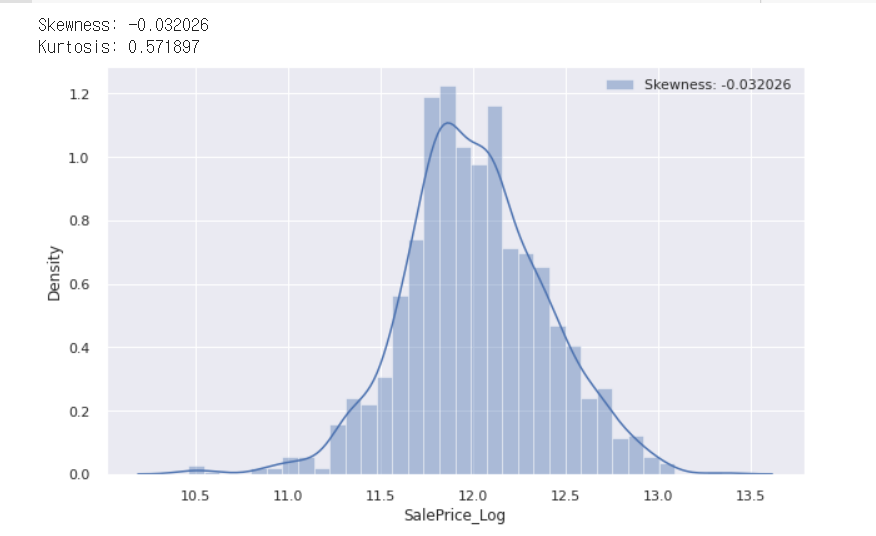
첫 번째 줄에서 시행한 것은 df_train에 새로운 열을 만드는 것으로, 'SalePrice' 열의 값이 0보다 클 경우, 해당 값의 로그 값을 저장하고, 0 이하인 경우에는 0을 저장한 값입니다. 이는 데이터의 skewness를 줄이는 역할을 합니다. 이 코드를 실행한 값을 확인하면 이전보다 훨씬 정규분포와 가까워진 것을 알 수 있습니다.
다른 변수들에서도 skewness와 kurtosis가 보였지만, 데이터 탐색 과정에서 주요 변수로 나타난 수치형 변수들은 skewness와 kurtosis가 수치적으로 보이지 않았습니다. 따라서 sale price만 로그를 취해 정규근사화 해줍니다.
- 결측 데이터 처리
집값 예측 문제에 많은 결측값들이 포함되어 있습니다. 하지만 이 결측값들은 관찰되지 않았다는 뜻이 아니라 있다, 없다의 개념입니다. 따라서 다음과 같은 과정을 수행합니다.
cols_fillna = ['PoolQC','MiscFeature','Alley','Fence','MasVnrType','FireplaceQu',
'GarageQual','GarageCond','GarageFinish','GarageType', 'Electrical',
'KitchenQual', 'SaleType', 'Functional', 'Exterior2nd', 'Exterior1st',
'BsmtExposure','BsmtCond','BsmtQual','BsmtFinType1','BsmtFinType2',
'MSZoning', 'Utilities']
for col in cols_fillna:
df_train[col].fillna('None',inplace=True)
df_test[col].fillna('None',inplace=True)위의 변수들은 결측값의 의미가 있다, 없다의 개념을 가지는 변수들입니다. 따라서 NaN 값을 없다의 뜻인 None으로 바꾸어줍니다. 이 과정에서 결측값을 특정 값으로 채워주는 df.fillna() 함수를 사용합니다.
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(5)
결측값의 총 개수와 그 비율을 missing_data에 저장하고 확인합니다. 이 과정을 통해 결측치의 처리 정도를 알 수 있습니다.
df_train.fillna(df_train.mean(), inplace=True)
df_test.fillna(df_test.mean(), inplace=True)
total = df_train.isnull().sum().sort_values(ascending=False)
percent = (df_train.isnull().sum()/df_train.isnull().count()).sort_values(ascending=False)
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(5)
위 처음 두 코드를 입력하여 데이터프레임의 평균치로 결측값들을 대체합니다. 그리고 다시 이전 코드와 같은 과정을 통해 결측치의 처리 정도를 확인해보면 결측값들이 사라진 것을 확인할 수 있습니다.
df_train.isnull().sum().sum(), df_test.isnull().sum().sum()각 데이터프레임의 결측치의 총합을 구하는 코드입니다. 첫 번째 sum()에서 각 열의 결측치를 합하고, 두 번째 sum()에서 모든 열의 결측치를 합하기 때문에 이 코드의 결과값은 결측치의 총합이라는 것을 알 수 있습니다. 그 결과는 (0,0)으로 결측값은 없다고 한 번 더 확인할 수 있습니다.
작성자 : 김윤섭
작성일 : 2023-03-28
진도 : Feature Engineering
id_test = df_test['Id']
to_drop_num = num_weak_corr
to_drop_catg = catg_weak_corr
cols_to_drop = ['Id'] + to_drop_num + to_drop_catg
for df in [df_train, df_test]:
df.drop(cols_to_drop, inplace= True, axis = 1)
우리가 원하는 것은 여러 변수들을 통해 saleprice라는 변수를 예측하는 것이기 때문에 saleprice와의 상관관계가 약한 변수들은 삭제를 해주어야 합니다.
위 과정을 위해 df_test의 id열만을 추출하여 id_test 변수에 저장합니다. 상관관계가 약한 수치형 변수는 num_weak_corr에 범주형 변수는 catg_weak_corr에 각각 리스트 형태로 저장되어 있습니다. cols_to_drop에 id의 열과 삭제할 변수들의 값을 합쳐서 삭제할 열들의 리스트를 저장합니다. 이후 전체 데이터 프레임인 df_train과 df_test에서 cols_to_drop에 해당되는 모든 열들을 제거해줍니다.
df_train.head()
catg_list = catg_strong_corr.copy()
catg_list.remove('Neighborhood')
for catg in catg_list :
sns.violinplot(x=catg, y=df_train["SalePrice_Log"], data=df_train)
plt.show()위 과정에서 확인했던 saleprice와 상관관계가 컸던 범주형 변수들 중 범주가 너무 많은 Neighborhoood 변수만 제외하여 catg_list에 저장합니다. Neighborhoood 변수는 해당되는 요소가 너무 많기 때문에 그래프의 변형을 거쳐서 나타내 주어야 합니다. catg_list 리스트의 데이터를 활용하여 sns.violinplot 함수를 통해 바이올린 그래프를 그려주고 출력해봅니다.

위와 같은 바이올린 그래프 형태로 각 범주의 해당하는 그래프 9가지가 출력됩니다. 이를통해 각 범주형 변수별로 주택 가격의 분포가 어떤지 시각화하여 이해할 수 있습니다.
fig, ax = plt.subplots()
fig.set_size_inches(16, 5)
sns.violinplot(x='Neighborhood', y=df_train["SalePrice_Log"], data=df_train, ax=ax)
plt.xticks(rotation=45)
plt.show()Neighborhood 변수에는 범주가 너무 많기 때문에 plt.subplots 함수를 이용하여 그래프의 크기를 늘려줍니다. 또한 x축에 할당되는 범주들의 이름도 plt.xticks 함수를 이용하여 기울기를 바꾸어 가독성을 높인 그래프를 만들어줍니다. 이러한 과정을 지난 그래프를 출력해봅니다.

for catg in catg_list :
g = df_train.groupby(catg)["SalePrice_Log"].mean()
print(g)각 범주들의 Y값에 해당됐던 SlaePrice_Log 평균을 출력해봅니다.

위와 같은 형태로 catg_list에 있는 9가지의 변수별로 해당되는 범주들의 SlaePrice_Log 평균값이 출력됩니다.
# 'MSZoning'
msz_catg2 = ['RM', 'RH']
msz_catg3 = ['RL', 'FV']
# Neighborhood
nbhd_catg2 = ['Blmngtn', 'ClearCr', 'CollgCr', 'Crawfor', 'Gilbert', 'NWAmes', 'Somerst', 'Timber', 'Veenker']
nbhd_catg3 = ['NoRidge', 'NridgHt', 'StoneBr']
# Condition2
cond2_catg2 = ['Norm', 'RRAe']
cond2_catg3 = ['PosA', 'PosN']
# SaleType
SlTy_catg1 = ['Oth']
SlTy_catg3 = ['CWD']
SlTy_catg4 = ['New', 'Con']범주형 데이터들을 수치화하기 위해서 앞에서 보았던 violinplot과 houseprice log의 평균값을 토대로 비슷한 값을 가진 요소들 끼리 그룹화 시켜줍니다. 위와 같은 그룹화는 4가지의 범주형 데이터를 세분화하여 9가지의 새로운 그룹으로 만들어줍니다. 특정된 4가지 범주형 데이터는 요소의 개수가 많기 때문의 후에 작성할 코드의 길이를 효율적으로 작성하기 위하여 선택된 것입니다.
for df in [df_train, df_test]:
df['MSZ_num'] = 1
df.loc[(df['MSZoning'].isin(msz_catg2) ), 'MSZ_num'] = 2
df.loc[(df['MSZoning'].isin(msz_catg3) ), 'MSZ_num'] = 3
df['NbHd_num'] = 1
df.loc[(df['Neighborhood'].isin(nbhd_catg2) ), 'NbHd_num'] = 2
df.loc[(df['Neighborhood'].isin(nbhd_catg3) ), 'NbHd_num'] = 3
df['Cond2_num'] = 1
df.loc[(df['Condition2'].isin(cond2_catg2) ), 'Cond2_num'] = 2
df.loc[(df['Condition2'].isin(cond2_catg3) ), 'Cond2_num'] = 3
df['Mas_num'] = 1
df.loc[(df['MasVnrType'] == 'Stone' ), 'Mas_num'] = 2
df['ExtQ_num'] = 1
df.loc[(df['ExterQual'] == 'TA' ), 'ExtQ_num'] = 2
df.loc[(df['ExterQual'] == 'Gd' ), 'ExtQ_num'] = 3
df.loc[(df['ExterQual'] == 'Ex' ), 'ExtQ_num'] = 4
df['BsQ_num'] = 1
df.loc[(df['BsmtQual'] == 'Gd' ), 'BsQ_num'] = 2
df.loc[(df['BsmtQual'] == 'Ex' ), 'BsQ_num'] = 3
df['CA_num'] = 0
df.loc[(df['CentralAir'] == 'Y' ), 'CA_num'] = 1
df['Elc_num'] = 1
df.loc[(df['Electrical'] == 'SBrkr' ), 'Elc_num'] = 2
df['KiQ_num'] = 1
df.loc[(df['KitchenQual'] == 'TA' ), 'KiQ_num'] = 2
df.loc[(df['KitchenQual'] == 'Gd' ), 'KiQ_num'] = 3
df.loc[(df['KitchenQual'] == 'Ex' ), 'KiQ_num'] = 4
df['SlTy_num'] = 2
df.loc[(df['SaleType'].isin(SlTy_catg1) ), 'SlTy_num'] = 1
df.loc[(df['SaleType'].isin(SlTy_catg3) ), 'SlTy_num'] = 3
df.loc[(df['SaleType'].isin(SlTy_catg4) ), 'SlTy_num'] = 4
주택의 구역, 동네, 상태. 벽돌 타입, 외관 품질, 지하실의 퀄리티, 중앙 에어컨 유무, 전기 시스템, 주방의 퀄리티, 판매 타입 등 10개의 범주형 변수를 대상으로 각각의 수치형 변수를 할당하는 것입니다. 예를 들어 df[MSZ_num] 변수는 MSZoning에 속한 범주값을 기반으로 클수록 3 작을수록 1을 갖도록하여 비슷한 범주값을 가진 것들끼리 그룹화 시켜줍니다. 다른 열들에서는 변수의 갯수나 변수값의 분산의 정도가 크다면 변수 값을 0이나 4 등 더욱 다양한 변수값을 지정해 줍니다.
new_col_HM = df_train[['SalePrice_Log', 'MSZ_num', 'NbHd_num', 'Cond2_num', 'Mas_num', 'ExtQ_num', 'BsQ_num', 'CA_num', 'Elc_num', 'KiQ_num', 'SlTy_num']]
colormap = plt.cm.PuBu
plt.figure(figsize=(10, 8))
plt.title("Correlation of New Features", y = 1.05, size = 15)
sns.heatmap(new_col_HM.corr(), linewidths = 0.1, vmax = 1.0,
square = True, cmap = colormap, linecolor = "white", annot = True, annot_kws = {"size" : 12})
이제는 범주형 변수를 수치화 시킨 것들을 토대로 heat map을 그려보도록 할 것입니다. Heat map은 각 열들 끼리의 상관계수를 한눈에 파악할 수 있는 그래프 입니다. 그래프를 먼저 보겠습니다.

heat map은 new_col_HM의 각 열들을 x축과 y축에 두고 heat map의 행과 열끼리의 상관계수를 0~1사이의 값으로 나타내 줍니다. 상관계수가 높을수록 1에 가까우며 짙은 색으로 표현됩니다. 반대로 상관계수가 낮을수록 0에 가까우며 밝은 색으로 표현됩니다. 위에 데이터 전처리 과정의 범주형 변수를 수치화 하는 과정에서 0~4 사이의 정수 값을 부여했었습니다. new_col_HM의 각 열들끼리 비교 했을 때 요소들의 정수 값, 즉 수치화 된 값이 비슷한 것이 많을수록 상관계수가 높다고 평가할 수 있을 것입니다. 주택의 구역에서 높은 정수 값을 받은 요소가 지하실 퀄리티에서도 높은 정수 값을 받았고 반대로 낮은 정수 값을 받은 것 또한 겹친다면 통상적으로 둘의 상관관계가 높다고 생각할 수 있기 때문입니다. Heat map에서는 이러한 매커니즘을 통해 그래프를 시각적으로 나타내 줍니다.
작성자 : 박찬혁
작성일 : 2023-03-28
진도 : Feature Engineering (line 37 ~ line 39)

위 히트맵에서 유의하지 않는 요소들을 모두 삭제해줍니다. 위에서 보았을 때, NbHd_num, Ext_num, Bsq_num, KiQ_num이 유의하다고 볼 수 있습니다. (0.50 이상을 유의적이라고 봄)

drop 함수(pandas 라이브러리에서 제공하는 함수, 데이터프레임에서 행이나 열을 삭제하는 함수)를 이용하여 유의하지 않은 요소들을 삭제하였습니다.
df_train.head()
df_test.head()
.이후 head함수를 이용하여 어떻게 변환되었는지 확인합니다.
작성자 : 오동진
작성일 : 2023-03-26
진도 : Modeling & make submission
가장 먼저 학습에 사용할 모델은그레디언트 부스팅의 고급버전인 XGBoost입니다.
앙상블 기법은 여러개의 분류기를 생성하고, 그 예측을 결합함으로써 보다 정확한 예측을 도출하는 기법을 말합니다. 이는 강력한 하나의 모델을 사용하는 대신, 보다 약한 모델 여러 개를 조합하여 더 정확한 예측에 도움을 주는 방식입니다.
앙상블 기법은 일반적으로 보팅(Voting), 베깅(Bagging), 부스팅(Boosting)세 가지 유형으로 나눌 수 있습니다.
학습에 사용할 부스팅 방식은 오분류된 개체들에 집중해 새로운 분류 규칙을 만드는 단게를 반복하는 방법입니다. 즉 약한 예측 모형들을 결합하여 강한 예측 모형들을 결합하여 강한 예측 모형을 만드는 것이 바로 부스팅 알고리즘입니다.
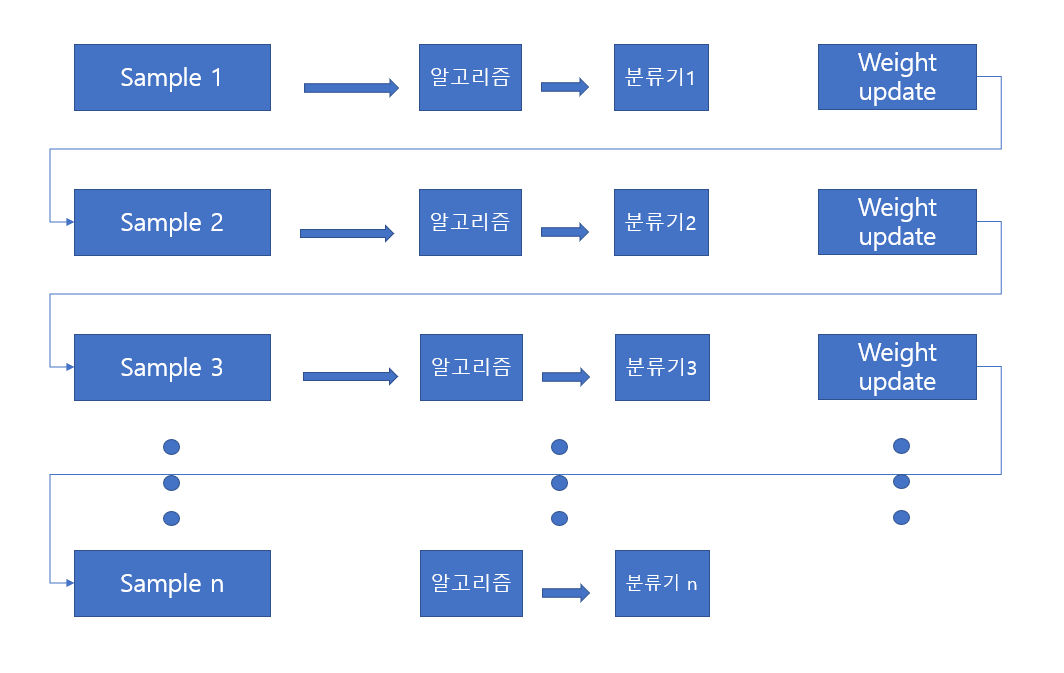
예측변수는 순차적으로 생성되며 원시 데이터의 객체들에는 동일한 가중치에서 시작하지만 모델링을 통한 예측변수에 의해 오분류된 개체들에는 높은 가중치를 부여하고, 정분류된 객체들에는 낮은 가중치를 부여하여 오분류된 객체들이 더 잘 분류되도록 하는 방법이 부스팅 방법입니다.
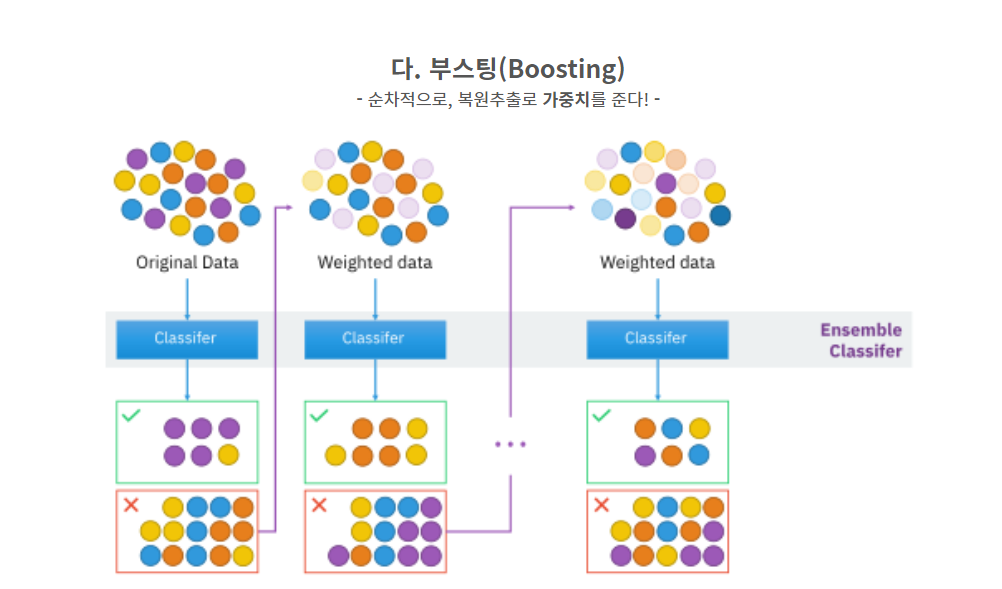
부스팅 방식 모델 중 에이다부스트는 새로운 트리가 이전 트리의 오차를 기반으로 가중치를 조정합니다. 에이다부스트는 실수를 통해 학습하는 방식이기 때문에 약한 학습기를 강력한 학습기로 만들 수 있습니다. 약한 학습기로 시작하는 이유는 부스팅 방식이 강력한 기반 모델을 만들기 보다는 반복적으로 오류를 고치는 데 초점을 맞추기 때문입니다. 기반 모델이 너무 강력하면 학습 과정이 제한되어 부스팅 모델 전략이 약화됩니다.
수백 번의 반복을 통해 약한 모델 강한 모델로 바뀌는 것입니다. 작은 성능 개선(낮은 가중치)을 오래 지속하는 것이 목표입니다.
그레디언트 부스팅은 이와 조금 다른 전략을 사용하는데 이전 트리의 예측 오차를 기반으로 완전히 새로운 트리를 만듭니다. 새로운 트리는 올바르게 예측된 값에는 영향을 받지 않습니다. 오차를 계산하는 방식은 모델의 예측과 실제 값 사이의 차이인 잔차(residual)를 활용합니다. 각 트리의 예측 값을 더해 모델 평가에 사용한다고 생각할 수 있습니다.
from sklearn.model_selection import train_test_split
from sklearn import metrics
X_train = df_train.drop("SalePrice_Log", axis = 1).values
target_label = df_train["SalePrice_Log"].values
X_test = df_test.values
X_tr, X_vld, y_tr, y_vld = train_test_split(X_train, target_label, test_size = 0.2, random_state = 2000)Scikit-learn 라이브러리에서 제공하는 train_test_split 함수를 사용하여 주어진 데이터셋을 학습 데이터와 검증 데이터로 나누는 역할을 합니다.
1. X_train : 학습 데이터셋에서 SalePrice_Log 컬럼을 제외한 모든 feature 값들을 담은 데이터셋입니다.
2. target_label : 학습 데이터셋에서 SalePrice_Log 컬럼 값들을 담은 데이터셋입니다.
3. X_test : 테스트 데이터셋의 feature 값들을 담은 데이터셋입니다.
4. X_tr, y_tr : 학습 데이터셋에서 X_train의 80%를 사용하여 학습한 모델을 만들기 위한 데이터셋입니다.
5. X_vld, y_vld : 학습 데이터셋에서 X_train의 20%를 사용하여 검증한 후 모델의 성능을 평가하기 위한 데이터셋입니다.
6. test_size : 학습 데이터셋에서 20%를 검증 데이터셋으로 사용하고자 한다는 의미입니다.
7. random_state : 랜덤 시드 값으로, 재현 가능한 결과를 얻기 위해 고정된 값을 사용합니다.

import xgboost
regressor = xgboost.XGBRegressor(colsample_bytree = 0.4603, learning_rate = 0.06, min_child_weight = 1.8,
max_depth= 3, subsample = 0.52, n_estimators = 2000,
random_state= 7, ntrhead = -1)
regressor.fit(X_tr,y_tr)XGBoost(Extreme Gradient Boosting) 라이브러리를 사용하여 Gradient Boosting 알고리즘을 적용한 회귀 모델을 만드는 역할을 합니다.
regressor = xgboost.XGBRegressor(...) : XGBRegressor 클래스를 사용하여 회귀 모델을 생성합니다.
colsample_bytree : 트리 생성 시 column을 샘플링하는 비율을 지정합니다.
learning_rate : 학습률을 지정합니다. 이 값은 각각의 부스팅 스텝에서 가중치를 얼마나 강하게 적용할 것인지를 결정합니다.
min_child_weight : 자식 노드에서 필요한 최소한의 샘플 개수를 지정합니다.
max_depth : 트리의 최대 깊이를 지정합니다.
subsample : 각각의 트리 생성 시에 사용될 샘플링 비율을 지정합니다.
n_estimators : 앙상블에서 사용할 트리의 개수를 지정합니다.
random_state : 랜덤 시드 값으로, 재현 가능한 결과를 얻기 위해 고정된 값을 사용합니다.
nthread : 사용할 스레드 수를 지정합니다. -1로 지정하면 가능한 모든 스레드를 사용합니다.
regressor.fit(X_tr, y_tr) : X_tr과 y_tr 데이터셋으로 모델을 학습합니다.
y_hat = regressor.predict(X_tr)
plt.scatter(y_tr, y_hat, alpha = 0.2)
plt.xlabel('Targets (y_tr)',size=18)
plt.ylabel('Predictions (y_hat)',size=18)
plt.show()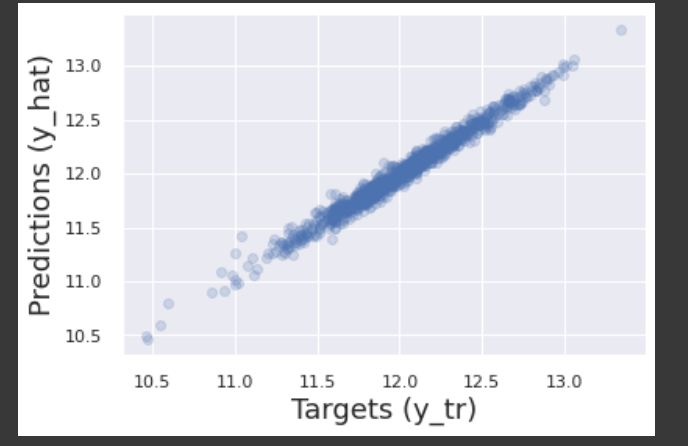
해당 코드는 회귀 모델을 학습한 후, 학습 데이터셋을 사용하여 예측한 결과값(y_hat)을 시각화하는 역할을 합니다.
1. y_hat = regressor.predict(X_tr) : X_tr 데이터셋으로 학습된 regressor 모델을 사용하여 예측값(y_hat)을 생성합니다.
2. plt.scatter(y_tr, y_hat, alpha = 0.2) : y_tr과 y_hat 값을 산점도(scatter plot)로 그립니다. alpha 값은 점의 투명도를 조절하는데 사용됩니다.
3. plt.xlabel('Targets (y_tr)',size=18) : x축 레이블을 'Targets (y_tr)'로 설정합니다.
4. plt.ylabel('Predictions (y_hat)',size=18) : y축 레이블을 'Predictions (y_hat)'로 설정합니다.
5. plt.show() : 그래프를 출력합니다. 이를 통해 실제값(y_tr)과 예측값(y_hat)의 분포를 시각적으로 확인할 수 있습니다.
regressor.score(X_tr,y_tr)0.9778929954593789`regressor.score(X_tr, y_tr)`는 학습된 회귀 분석 모델인 `regressor`에 대해, 학습용 데이터 `X_tr`과 `y_tr`을 사용하여 모델을 평가하는 코드입니다.
이 코드는 회귀 분석 모델의 결정 계수(R-squared) 값을 반환합니다. 결정 계수는 모델이 주어진 데이터를 얼마나 잘 설명하는지를 나타내는 지표입니다.
결정 계수는 0에서 1사이의 값을 가지며, 1에 가까울수록 모델이 입력 변수의 변동을 타깃 변수의 변동으로 잘 설명한다는 것을 의미합니다. 반면, 0에 가까울수록 모델이 입력 변수의 변동과 타깃 변수의 변동 사이에 관계를 찾지 못한다는 것을 의미합니다.
따라서, `regressor.score(X_tr, y_tr)` 값이 높을수록 모델이 주어진 데이터를 잘 설명한다는 것을 의미합니다. 하지만, 이 값이 높다고 해서 항상 모델이 좋다는 것은 아닙니다. 새로운 데이터에 대해서도 모델이 잘 동작하는지를 확인해야 합니다.
y_hat_test = regressor.predict(X_vld)
plt.scatter(y_vld, y_hat_test, alpha=0.2)
plt.xlabel('Targets (y_vld)',size=18)
plt.ylabel('Predictions (y_hat_test)',size=18)
plt.show()

이 코드는 학습된 회귀 분석 모델을 사용하여 검증용 데이터 `X_vld`에 대한 예측값 `y_hat_test`을 계산하고, 이를 산점도로 시각화합니다.
산점도의 x축은 검증용 데이터의 실제값 `y_vld`를 나타내고, y축은 모델이 예측한 값 `y_hat_test`를 나타냅니다.
따라서, 산점도의 점들이 대각선 y=x에 가깝게 모여 있을수록 모델이 검증용 데이터를 잘 예측했다는 것을 의미합니다. 산점도에서 점들이 대각선 y=x에서 멀리 떨어져 있거나, 어떤 패턴을 가지고 분포하고 있다면, 모델의 예측이 부정확하거나 일부 입력 변수에 대해 모델이 잘못 학습되었을 가능성이 있습니다.
따라서, 산점도를 통해 모델이 검증용 데이터에 대해 얼마나 정확한 예측을 하는지, 어떤 입력 변수에 대해 모델이 잘못 예측하는지 등을 파악할 수 있습니다.
regressor.score(X_vld,y_vld)0.8387039163837681x_tr, y_tr과 마찬가지로 모델을 평가해줍니다.
from sklearn.model_selection import cross_val_score
accuracies = cross_val_score(estimator = regressor, X = X_tr, y = y_tr, cv = 10)이 코드는 `sklearn` 패키지에서 제공하는 `cross_val_score` 함수를 사용하여, 회귀 분석 모델의 성능을 교차 검증을 통해 평가하는 작업을 수행합니다.
`cross_val_score` 함수의 인자로는 다음과 같은 값이 사용됩니다.
- `estimator`: 회귀 분석 모델 객체
- `X`: 입력 변수 데이터셋
- `y`: 목표 변수 데이터셋
- `cv`: 교차 검증을 위한 fold 수
이 함수는 `cv` 개의 fold로 데이터셋을 분할하고, 각각의 fold를 검증용 데이터셋으로 사용하여 모델을 학습하고 평가합니다. 이를 `cv`번 반복하여 모델의 성능을 평균적으로 계산합니다.
이 코드에서는 `regressor`라는 회귀 분석 모델을 사용하고, `X_tr`과 `y_tr`은 학습용 데이터셋입니다. `cv`는 10으로 설정되어 있으므로, 데이터셋을 10개의 fold로 분할하여 교차 검증을 수행합니다.
`cross_val_score` 함수의 결과로 반환되는 `accuracies`는 각 fold에서 모델의 성능을 나타내는 평가 지표의 배열입니다. 이 배열을 평균하여 모델의 전체적인 성능을 계산할 수 있습니다.
print(accuracies.mean())
print(accuracies.std())
# 정확도를 확인해봅니다.0.8463773269333027
0.03393380365418177use_logvals = 1
pred_xgb = regressor.predict(X_test)
sub_xgb = pd.DataFrame()
sub_xgb['Id'] = id_test
sub_xgb['SalePrice'] = pred_xgb
if use_logvals == 1:
sub_xgb['SalePrice'] = np.exp(sub_xgb['SalePrice'])
sub_xgb.to_csv('xgb.csv',index=False)
# use_logvals는 Log를 취해준 Target feature을 exp해주기 위해 사용되는 스위치 역할입니다.
# 제대로 된 예측을 위해 학습 후 Log변환을 풀어줘야하기 때문입니다.
# 이 셀의 코드를 통해 submission까지 완료하게됩니다.
이 코드는 학습된 XGBoost 회귀 분석 모델을 사용하여 테스트 데이터셋 `X_test`에 대한 예측값을 계산하고, 이를 `sub_xgb` 데이터프레임에 저장하고, CSV 파일로 저장하는 작업을 수행합니다.
먼저, `regressor.predict(X_test)`를 사용하여 `X_test`에 대한 예측값을 계산하고, 이를 `pred_xgb`에 저장합니다.
그리고 `sub_xgb` 데이터프레임을 생성합니다. 이 데이터프레임은 `Id`와 `SalePrice` 두 개의 컬럼으로 구성됩니다. `Id` 컬럼에는 `id_test` 배열의 값이, `SalePrice` 컬럼에는 `pred_xgb` 배열의 값이 저장됩니다.
만약 `use_logvals` 변수의 값이 1이라면, `sub_xgb` 데이터프레임의 `SalePrice` 컬럼에 저장된 값에 `np.exp()` 함수를 적용하여 로그 값에서 원래의 값으로 변환합니다.
마지막으로, `sub_xgb` 데이터프레임을 `xgb.csv` 파일로 저장합니다. 이때 `index=False` 옵션을 사용하여 인덱스 정보는 CSV 파일에 저장하지 않습니다.
House Price (Advanced)
https://www.kaggle.com/code/subinium/subinium-tutorial-house-prices-advanced/notebook
위에 서술된 beginner 단계를 통해 주택 가격 예측을 공부했습니다. 위에 서술된 과정에서는 주택 가격을 예측할 때 XGBoost 모델을 사용했는데 '다른 모델을 사용하면 더 좋은 결과를 낼 수 있지 않을까?'라는 생각이 들었습니다. 그래서 동일한 주제를 가지고 다른 모델을 사용한 글을 추가적으로 살펴봤습니다. 그 결과 LightGBM을 사용하여 주택 가격을 예측한 글을 찾을 수 있었습니다. 아래는 beginner 단계와의 차이점을 위주로 LightGBM을 사용한 커널을 설명한 내용입니다.
작성자 : 박시현
작성일 : 2023-04-03
진도 :
- 이상치 탐색 및 제거
#이상치 탐색
fig, ax = plt.subplots()
ax.scatter(x=train_df['GrLivArea'], y=train_df['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()
#이상치 제거
train_df = train_df.drop(train_df[(train_df['GrLivArea']>4000) & (train_df['SalePrice']<300000)].index)
#Check the Graph again
fig, ax = plt.subplots()
ax.scatter(x=train_df['GrLivArea'], y=train_df['SalePrice'])
plt.ylabel('SalePrice', fontsize=13)
plt.xlabel('GrLivArea', fontsize=13)
plt.show()

y축을 SalesPrice로 두고 x축을 GrLivArea로 설정합니다. 이렇게 설정한 그래프의 결과값은 위와 같습니다. 그래프를 보면 SalesPrice<300000이고 GrLivArea>4000인 곳에 이상치가 존재합니다. 이상치를 제거해줍니다.

이상치 제거 후 그래프입니다. 이상치들이 삭제된 것을 알 수 있습니다. Beginner 단계에서는 이상치의 결과값을 구하고 이 값에 해당하는 122개의 행들을 전부 삭제했는데, advanced 레벨에서 그렇게 하지 않은 이유는 다음과 같습니다.
- 훈련 데이터말고 테스트 데이터에도 이상치들이 있을 수 있다.
- 그렇다면 이상치들을 전부 삭제하는 것이 오히려 모델에 악영향을 줄 수 있다.
이런 이유들 때문에 모든 이상치를 제거하지 않고 모델에서 이런 데이터들을 제어할 것입니다.
Beginner level과 비슷하게 데이터를 정규화, 결측값 처리, 범주형 데이터 라벨링을 해줍니다.
all_data['TotalSF'] = all_data['TotalBsmtSF'] + all_data['1stFlrSF'] + all_data['2ndFlrSF']Sale Price와 가장 관련 있는 변수 중 한 가지는 집의 가용 평수입니다. 그래서 집의 Basement 면적과 1층, 2층 면적을 합쳐서 새로운 'TotalSF'변수에 저장해줍니다.
초급자 과정에서는 주택 가격과 밀접히 관련이 있는 변수들의 Skewness와 Kortosis가 수치적으로 보이지 않는다는 이유로 정규화를 하지 않았습니다. 반면 상급자 과정에서는 Box-Cox Transformation을 이용해 수치형 데이터를 정규분포 형태로 바꿔줍니다.
skewness = skewness[abs(skewness) > 0.75]
print("There are {} skewed numerical features to Box Cox transform".format(skewness.shape[0]))
from scipy.special import boxcox1p
skewed_features = skewness.index
lam = 0.15
for feat in skewed_features:
all_data[feat] = boxcox1p(all_data[feat], lam)왜도가 0.75보다 큰 feature들을 선택하여 Box Cox 변환을 적용합니다.
작성자 : 김윤섭
작성일 : 2023-04-04
진도 : Modeling by LightGMB
우리가 사용할 LightGMB 모델은 XGBoost 모델에 비해 상황에 따라 좋은 점도 있지만 나쁜 점도 있습니다. 따라서 모델을 설정할 때 우리가 가진 데이터의 크기, 데이터 형태, 데이터의 지저분한? 정도 등의 상황을 고려해야 합니다.
먼저 LightGMB의 특징을 살펴 보겠습니다. LightGMB은 XGBoost와 마찬가지로 Gradient Boosting 알고리즘을 기반으로 작동합니다. Gradent Boosting가 무엇이냐하면 하나의 모델을 통해 오차를 줄여나가는 일반적인 Decision Tree와는 다른 하나의 모델을 학습한 후 또 다른 모델을 이용하여 오차를 줄여나가는 방법 입니다. 즉 위에서도 언급 되었던 앙상블 학습방법 중에 하나입니다.
XGBoost와 크게 다른 점은 Histogram-based 알고리즘을 이용한다는 점입니다. 히스토그램 알고리즘은다른 알고리즘에 비해 더욱 빠르고 정확하다는 것과 Categorical Feature의 처리가 효율적이라는 장점이 있으나 한정적인 환경에서만 적용됩니다. 일단 과적합(학습 데이터를 과도하게 학습하여 오히려 예측력이 떨어지는 현상) 현상이 고차원 데이터 환경에서 일어날 확률이 높습니다. 두번째로 대규모의 데이터셋에서만 장점이 발휘 됩니다. 마지막으로 데이터의 분포가 고르지 않다면, 즉 잘 정제된 데이터가 아니라면 모델의 성능이 크게 저하됩니다.
우리가 가진 데이터인 Boston House Price 데이터가 LightGMB 모델에 적합한지 판단 해보겠습니다. Boston 데이터는 대규모의 데이터 입니다. 미국 Boston 지역의 집들의 주거환경이나 주거지의 특징을 모두 담은 데이터이기 때문입니다. 수치형 변수도 있지만 범주형(Categorical) 변수도 굉장히 많습니다. 또한 13개의 feature로 이루어져 있기 때문에 고차원적인 데이터라고 할 수도 없습니다. 마지막으로 Boston 데이터의 분포가 고른지는 답을 하기가 쉽지는 않습니다. 데이터를 잘 정제(인덱싱)할수록 LightGMB 모델의 능률이 높아질 것이기 때문입니다. 따라서 이상치 제거 등의 작업 등을 통해서 모델을 더욱 효과적으로 사용하는 것이 올바른 방향일 것입니다. 결과적으로 이야기 해보면 Boston House Price 데이터는 LightGMB 모델을 도입하기에 적합하고 XGBoost 보다 효과적인 모델이 될 수 있다고 생각합니다.
line 36)
import lightgbm as lgb일단 LightGMB 라이브러리를 import 하겠습니다.
line 42)
model_lgb = lgb.LGBMRegressor(objective='regression',num_leaves=5,
learning_rate=0.05, n_estimators=720,
max_bin = 55, bagging_fraction = 0.8,
bagging_freq = 5, feature_fraction = 0.2319,
feature_fraction_seed=9, bagging_seed=9,
min_data_in_leaf =6, min_sum_hessian_in_leaf = 11)이 코드는 LightGMB 알고리즘을 이용하여 LGBMRegressor 모델을 정의하는 코드입니다. 모델을 정의한다는 것은 모델의 하이퍼 파라미터(모델을 학습시킬 때 조절가능한 파라미터)를 정의하는 것과 같습니다.
- objective: 손실 함수입니다. 여기서는 회귀 문제이므로 'regression'으로 설정되어 있습니다.
- num_leaves: 트리에 존재하는 최대 잎의 수입니다.
- learning_rate: 경사 하강법에서 사용되는 학습률입니다.
- n_estimators: 트리의 수입니다.
- max_bin: 최대 bin의 수입니다.
- bagging_fraction: 훈련 데이터에서 데이터 샘플링할 때 사용되는 비율입니다.
- bagging_freq: 데이터 샘플링을 수행하는 빈도입니다.
- feature_fraction: feature 샘플링 비율입니다.
- feature_fraction_seed: feature 샘플링에 사용되는 시드 값입니다.
- bagging_seed: 데이터 샘플링에 사용되는 시드 값입니다.
- min_data_in_leaf: 각 잎에 포함되는 최소 데이터 수입니다.
- min_sum_hessian_in_leaf: 최소 hessian 합계입니다.
위 설명은 이 모델의 하이퍼 파라미터를 설명한 것입니다.
line 48)
모델을 생성 했으니 모델의 예측력이 얼마나 정확한지 성능을 테스트 해보겠습니다.
score = rmsle_cv(model_lgb)
print("LGBM score: {:.4f} ({:.4f})\n" .format(score.mean(), score.std()))
위 코드는 모델의 성능을 알아보기 위해 교차 검증을 하는 과정입니다. 이 과정은 LGBMRegressor 모델의 rmsle의 값의 평균과 표준편차를 계산합니다. rmsle은 Boston House Price의 실제 값과 LGBMRegressor 모델의 예측 값의 차를 계산하여 예측 정확도를 계산하는 것입니다. 따라서 rmsle의 값이 작을수록 예측력이 높다고 볼 수 있습니다.
LGBM score: 0.1167 (0.0072)
출력값은 0.1167이 나왔습니다. 그렇다면 XGBoost의 rmsle의 값은 어떨지 보겠습니다.
model_xgb = xgb.XGBRegressor(colsample_bytree=0.4603, gamma=0.0468,
learning_rate=0.05, max_depth=3,
min_child_weight=1.7817, n_estimators=2200,
reg_alpha=0.4640, reg_lambda=0.8571,
subsample=0.5213, silent=1,
random_state =7, nthread = -1)score = rmsle_cv(model_xgb)
print("Xgboost score: {:.4f} ({:.4f})\n".format(score.mean(), score.std()))
Xgboost score: 0.1162 (0.0078)
XGBoost는 0.1162이 나왔습니다. 예상과는 다르게 XGBoost의 값이 더 적게 나왔으나 LightGMB 알고리즘을 이용한 모델도 거의 비슷한 퍼포먼스를 보여주었다고 할 수 있겠습니다.
'Study > Kaggle competition' 카테고리의 다른 글
| Kaggle competiton #1 : Titanic survivor predictions (0) | 2023.04.12 |
|---|---|
| Kaggle Competition #4 (1) | 2023.04.04 |
| kaggle competition #3 (0) | 2023.04.03 |
| Kaggle competition #2 (0) | 2023.04.03 |



