창원시의 인구 추이 예측을 통한 지방 소멸 문제 제고

배경 및 필요성

우리 조는 창원시의 여러 사회적 문제 중에서 '지방 소멸 위기'에 주목하였다. 창원시가 2022년에 특례시로 지정되었는데, 이 기준은 인구 100만 이상의 대도시이다. 그러나 창원시는 지속적으로 인구가 감소하고 있어서 10년 안에 특례시 지위를 반납해야 될 위기에 처하게 되었다.

 

우리는 인구 감소의 근본적인 원인을 '청년층 인구의 감소'로 지목하였다. 청년층 인구의 감소는 '인구 유출 문제'와 '자연적 인구 감소 문제'를 야기한다. 또한 창원시는 대한민국에서 성비 불균형이 가장 극심한 도시 중 하나이고, 이 문제가 청년층 인구 감소와 상관관계를 가지고 있다는 것을 전제로 분석을 진행하였다.

 

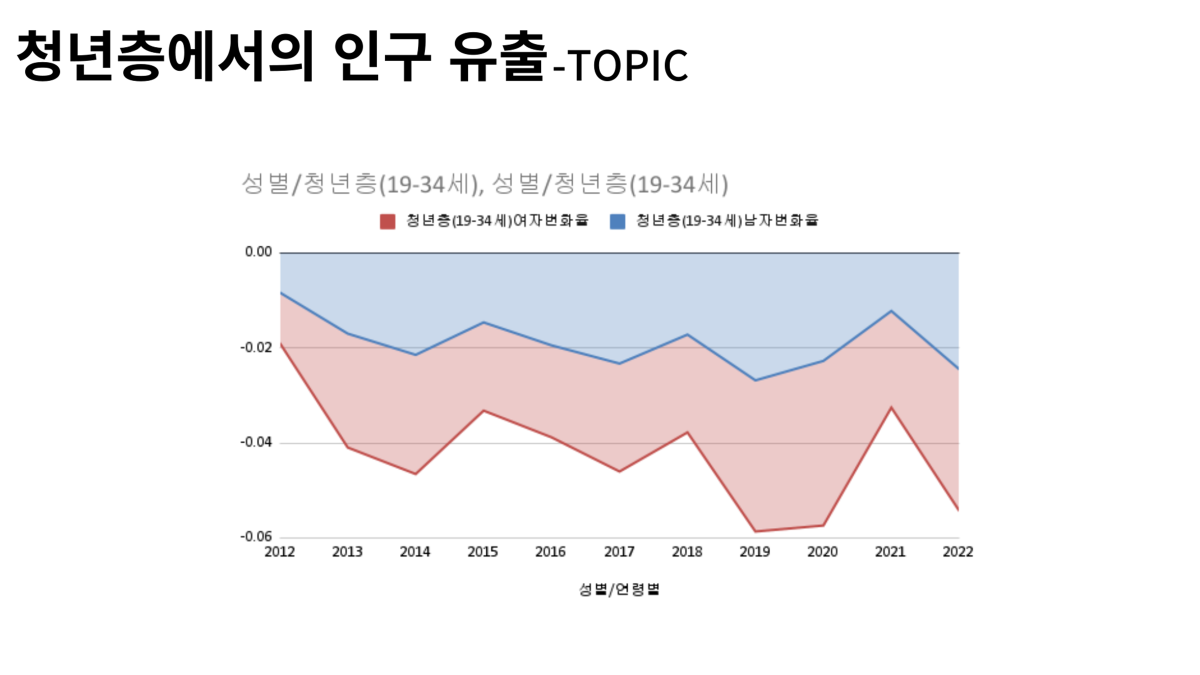
특히 청년층에서의 인구 유출이 심각하였다. 청년층이 일자리, 혼인 등의 이유로 창원을 떠나 수도권이나 다른 영남 대도시로 유출되고 있다. 이 현상은 성비 불균형도 가속화하는데, 청년층 여성에서 이탈이 더욱 두드러지게 나타나기 때문이다. 따라서 창원시의 미래 전출입 인구를 예측하고, 문제점을 파악한 후, 이를 해결하기 위한 제도적 방안이 필요하다고 판단했다.

청년층 인구 감소가 야기하는 자연적 인구 감소 문제도 심각하다. 창원시는 공업 기반 도시이기 때문에 타 대도시에 비하여 성비 불균형 지수가 높고, 이것이 청년층 인구감소 문제와 맞물려 자연적 인구 감소 문제를 가속화한다.

즉, 결혼 적령기 청년층 인구 자체도 감소하는데, 남성 인구에 비해 결혼할 여성 인구가 적으므로 혼인율이 지속적으로 감소한다. 결혼을 하지 않으니 연쇄적으로 출산율도 더욱 낮아질 것이고, 결국 사망사 수가 출생자 수보다 더 탄력적으로 증가하여 자연적 인구 감소 문제를 가속화할 것으로 보인다.

 

분석 데이터

 

실제 창원시 인구데이터의 차분 전후 ACF, PACF 그래프

ARIMA(AutoRegressive Integrated Moving Average)는 시계열 데이터 분석을 위한 통계적 모델입니다. ARIMA 모델은 시계열 데이터가 가지는 추세, 계절성, 불규칙성 등을 분석하고 예측하는 데 사용됩니다.

ARIMA의 전체적인 과정은 다음과 같습니다.

1.     데이터를 뽑아보고 정상성을 가졌는지 본다

2.     눈으로 불가능하면 Autocorrelation function을 통해 확인(ACF그래프)

3.     nonstationary이면 differencing 한다.

4.     differencing한 데이터를 다시한번 ACF로 확인한다. (2차 차분 결정)

5.     ACF, PACF를 보고 모델 설정

6.     AIC 값을 보고 P또는 Q값을 조정, AIC가 가장 낮을때의 P,Q값 확정

7.     PDQ가 확정돠고 ARIMA 예측 모델을 사용한다.

정상성이란 유동적이지 않은 변화가 있는 성질입니다. 예를 들어 평균이 일정하거나 0일 때, 분산이 일정할 때(시간이 지나도 퍼지는 정도가 일정)입니다. 그렇다면 데이터의 정상성은 어떻게 확인할까? 눈으로 확인이 가능하면 좋겠으나 대부분의 데이터는 그래프가 매끈하지 않습니다. 따라서 눈으로만 정상성을 판단하기에는 애매한 부분이 있어 ACF 그래프를 활용합니다. ACF (Autocorrelation Function) 란 각 차시에서 현재 차시와 얼마의 관계성을 갖는지 표현한 그래프 입니다. ACF를 보았을 때 정상성을 가지지 못하고 있다면 차분 과정을 통해 정상성을 만들어주어야 합니다. d차 차분이란 현시점 데이터에서 d시점 이전 데이터를 뺀 것입니다. 1차 차분을 시행한 후 2차, 3차 시행이 가능합니다. 보통 2차 차분부터는 ARIMA에 적합하지 않은 데이터라고 판단하기 때문에 1차 차분만 하는 경우가 많습니다.

차분 공식

위 창원시 인구데이터의 ACF, PACF 그래프는 1차 차분을 한 경우 정상성이 나타났기에 1차 차분만 하였습니다.

 

MA, AR, ARMA 모델 특징

 

ACF, PACF그래프 형태별 적합한 모델

ARIMA 모델을 사용하기 위해선 P, Q, D를 특정해야한다. P(자기회귀 차수):P는 모델이 고려하는 시차(lag)의 수를 나타냅니다. PACF(Partial Autocorrelation Function) 플롯을 사용하여 결정합니다. 플롯에서 유의미하게 0이 아닌 지점을 찾아 P값을 결정합니다. Q(Moving Average): Q는 모델의 이동평균 부분에서 고려하는 시차의 수를 의미합니다. ACF플롯을 사용하여 결정합니다. 마찬가지로 플롯에서 유의미하게 0이 아닌 지점을 찾아 Q값을 결정합니다. D는 차분의 개수에 따라 결정 됩니다. 따라서 저희가 선정한 값들은 P는 1, Q는 2, D는 1로 설정하여 ARIMA 모델을 돌려보았습니다. MSE (평균 제곱 오차와 RMSE (제곱근 평균 제곱 오차)를 구했을 때 0.1257와 0.1532 정도의 수치가 나왔으므로 유의미한 결과가 나왔다고 판단할 수 있다. 하지만 저희가 구한 창원시 시계열 데이터의 양이 적기 때문에 현재 시점에서 2년치 정도의 데이터만을 예측할 수 있었습니다. 

 

조사 방법

2010년 ~ 2022년의 월별, 성별, 연령별, 전입출, 사망 데이터를 바탕으로 ARIMA 알고리즘을 활용하여 2023년 ~ 2032년 월별, 성별, 연령별, 전입출, 사망 예측값을 도출했다. 이를 바탕으로 특정 년도 출생인들의 인구 추이를 각 연도에 해당 출생인들이 되는 나이의 예측값을 바탕으로 예측할 수 있다.

예를 들어, 00년생들의 인구 추이를 예측하려면, 그들이 20세가 되는 2020년의 20세 인구 추이값을 사용하고, 21세가 되는 2021년의 21세 인구 추이값을 사용한다. 이를 연쇄적으로 반영하여 결국 그들이 32살이 되는 2032년까지의 32살의 예측값을 활용한다.

 

결과 해석 및 시사점

시간 관계상 모든 row를 가지고 ARIMA를 돌리지 못했다.

 

이 모든 알고리즘을 돌리면 결국 남는 결과물은 '창원시의 인구 추이'이다. 얼마나 줄어들지의 예측값을 얻을 수 있고, 성비 불균형과의 관계를 더 명확하게 알 수 있다.

지금은 일부 데이터들을 통하여 ARIMA 알고리즘이 잘 작동하고, 예측을 원활하게 하는지 확인하였다.

 

활용방안과 기대효과

인구 감소 추세를 수치적으로 확인 가능할 수 있고, 미래를 예측하여 나이 별 인구 수가 어떻게 될 지 1살 단위로 미시적으로 확인할 수 있다.

이를 바탕으로 청년층의 이탈을 막고, 출산율과 혼인율을 높이는 정책을 디자이닝하는 데에 도움을 줄 수 있음